题目内容
 如图,在平面直角坐标系xOy中,抛物线y=
如图,在平面直角坐标系xOy中,抛物线y=
| ||
| 5 |
| 3 |
(1)求抛物线的解析式;
(2)若点P的横坐标为m,△PCD的面积为S,求S与m之间的函数关系式;
(3)过点P作PE⊥DP,连接DE,F为DE的中点,试求线段BF的最小值.
考点:二次函数综合题
专题:
分析:(1)将点A(1,0),B(0,
)代入y=
(x2+bx+c),运用待定系数法即可求出抛物线的解析式;
(2)先由抛物线的解析式求出对称轴为x=3,得到C点坐标(3,0),在Rt△OBC中,利用正切函数的定义得出tan∠OCB=
=
,于是∠OCB=30°,则∠PCD=60°,再证明△PCD是等边三角形,过点P作PQ⊥x轴于点Q,PG∥x轴,交CD于点G,求出CP=
=CD,PG=CQ=3-m,然后根据S△PCD=
CD•PG即可求出S与m之间的函数关系式;
(3)连结PF、CF,先利用SSS证明△CPF≌△CDF,得出∠PCF=∠DCF,由角平分线的定义可知点F在∠PCD的角平分线上,根据垂线段最短得出BF的最小值为点B到直线CF的距离,再根据角平分线的性质得到点B到直线CF的距离等于OB,进而求出线段BF的最小值.
| 3 |
| ||
| 5 |
(2)先由抛物线的解析式求出对称轴为x=3,得到C点坐标(3,0),在Rt△OBC中,利用正切函数的定义得出tan∠OCB=
| OB |
| OC |
| ||
| 3 |
2
| ||
| 3 |
| 1 |
| 2 |
(3)连结PF、CF,先利用SSS证明△CPF≌△CDF,得出∠PCF=∠DCF,由角平分线的定义可知点F在∠PCD的角平分线上,根据垂线段最短得出BF的最小值为点B到直线CF的距离,再根据角平分线的性质得到点B到直线CF的距离等于OB,进而求出线段BF的最小值.
解答:解:(1)∵抛物线y=
(x2+bx+c)过点A(1,0),B(0,
),
∴
,
解得
,
∴抛物线的解析式为y=
(x2-6x+5),
即y=
x2-
x+
;
(2)∵y=
x2-
x+
=
(x-3)2-
,
∴抛物线的对称轴为x=3,
∴C(3,0),
∵B(0,
),
∴OC=3,OB=
,
∴tan∠OCB=
=
,
∴∠OCB=30°,
∴∠PCD=60°.
∵∠CPD=60°,
∴∠CDP=60°,
∴△PCD是等边三角形.
 如图1,过点P作PQ⊥x轴于点Q,PG∥x轴,交CD于点G,
如图1,过点P作PQ⊥x轴于点Q,PG∥x轴,交CD于点G,
∵点P的横坐标为m,
∴OQ=m,CQ=3-m.
∴CP=
=CD,PG=CQ=3-m.
∴S△PCD=
CD•PG=
×
×(3-m)=
(3-m)2,
即S=
m2-2
m+3
(m<3);
 (3)如图2,连结PF、CF.
(3)如图2,连结PF、CF.
∵PE⊥DP,F为DE的中点,
∴PF=
DE=DF.
在△CPF与△CDF中,
,
∴△CPF≌△CDF(SSS),
∴∠PCF=∠DCF,
∴点F在∠PCD的角平分线上,
∴BF的最小值为点B到直线CF的距离.
∵∠OCB=∠BCF=30°,
∴点B到直线CF的距离等于OB,
∴BF的最小值为
.
| ||
| 5 |
| 3 |
∴
|
解得
|
∴抛物线的解析式为y=
| ||
| 5 |
即y=
| ||
| 5 |
6
| ||
| 5 |
| 3 |
(2)∵y=
| ||
| 5 |
6
| ||
| 5 |
| 3 |
| ||
| 5 |
4
| ||
| 5 |
∴抛物线的对称轴为x=3,
∴C(3,0),
∵B(0,
| 3 |
∴OC=3,OB=
| 3 |
∴tan∠OCB=
| OB |
| OC |
| ||
| 3 |
∴∠OCB=30°,
∴∠PCD=60°.
∵∠CPD=60°,
∴∠CDP=60°,
∴△PCD是等边三角形.
 如图1,过点P作PQ⊥x轴于点Q,PG∥x轴,交CD于点G,
如图1,过点P作PQ⊥x轴于点Q,PG∥x轴,交CD于点G,∵点P的横坐标为m,
∴OQ=m,CQ=3-m.
∴CP=
2
| ||
| 3 |
∴S△PCD=
| 1 |
| 2 |
| 1 |
| 2 |
2
| ||
| 3 |
| ||
| 3 |
即S=
| ||
| 3 |
| 3 |
| 3 |
 (3)如图2,连结PF、CF.
(3)如图2,连结PF、CF.∵PE⊥DP,F为DE的中点,
∴PF=
| 1 |
| 2 |
在△CPF与△CDF中,
|
∴△CPF≌△CDF(SSS),
∴∠PCF=∠DCF,
∴点F在∠PCD的角平分线上,
∴BF的最小值为点B到直线CF的距离.
∵∠OCB=∠BCF=30°,
∴点B到直线CF的距离等于OB,
∴BF的最小值为
| 3 |
点评:本题是二次函数的综合题型,其中涉及到运用待定系数法求抛物线的解析式,二次函数的性质,正切函数的定义,等边三角形的判定与性质,三角形的面积,直角三角形的性质,全等三角形的判定与性质,角平分线的定义与性质等知识,综合性较强,有一定难度.根据垂线段最短得出BF的最小值为点B到直线CF的距离是解决第(3)小题的关键.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
下列说法正确的是( )
| A、三角形的角平分线是射线 |
| B、过三角形的顶点,且过对边中点的直线是三角形的一条中线 |
| C、一个三角形同一边上的中线、高及这条边所对的角的平分线中,高最短 |
| D、三角形的高、中线、角平分线一定在三角形的内部 |
 m与n表示在数轴上的位置如图所示,则|m-n|化简结果为( )
m与n表示在数轴上的位置如图所示,则|m-n|化简结果为( )| A、m+n | B、m-n |
| C、n-m | D、-m-n |
过同一平面内的三点,可以画直线的条数是( )
| A、1 | B、3 | C、1或3 | D、无法确定 |

 解不等式组:
解不等式组: 如图,△ABC为等边三角形,D为BC边上一点,以AD为边作∠ADE=60°,DE与△ABC的外角平分线CE交于点E.
如图,△ABC为等边三角形,D为BC边上一点,以AD为边作∠ADE=60°,DE与△ABC的外角平分线CE交于点E.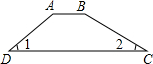 随着“碰瓷”事件的频繁发生,现在老人摔倒了敢不敢扶成了一个热门话题,前段时间郑州市的一群老人针对这个现象进行了一场名为“请放心扶起我”的行为艺术,为了扩大行为艺术的影响,纠正社会风气,某老年艺术团准备举行一场义演,请你为义演舞台的选址出谋划策,如图:舞台宽度为5米,左面楼梯长3米,梯面与地面夹角∠1为40°,右面有个专供残疾演员登台用的斜坡,与地面夹角∠2为30°,且台面AB与地面DC平行,请你通过计算说明至少空地面有多宽才能搭建下这个舞台(结果保留两位小数)?(
随着“碰瓷”事件的频繁发生,现在老人摔倒了敢不敢扶成了一个热门话题,前段时间郑州市的一群老人针对这个现象进行了一场名为“请放心扶起我”的行为艺术,为了扩大行为艺术的影响,纠正社会风气,某老年艺术团准备举行一场义演,请你为义演舞台的选址出谋划策,如图:舞台宽度为5米,左面楼梯长3米,梯面与地面夹角∠1为40°,右面有个专供残疾演员登台用的斜坡,与地面夹角∠2为30°,且台面AB与地面DC平行,请你通过计算说明至少空地面有多宽才能搭建下这个舞台(结果保留两位小数)?(