题目内容
20.四边形ABCD是菱形,∠BAD=60°,AB=6,对角线AC与BD相交于点O,点E在AC上,若OE=$\sqrt{3}$,则CE的长为4$\sqrt{3}$或2$\sqrt{3}$.分析 由菱形的性质证出△ABD是等边三角形,得出BD=AB=6,OB=$\frac{1}{2}$BD=3,由勾股定理得出OC=OA=$\sqrt{A{B}^{2}-O{B}^{2}}$=3$\sqrt{3}$,即可得出答案.
解答  解:∵四边形ABCD是菱形,
解:∵四边形ABCD是菱形,
∴AB=AD=6,AC⊥BD,OB=OD,OA=OC,
∵∠BAD=60°,
∴△ABD是等边三角形,
∴BD=AB=6,
∴OB=$\frac{1}{2}$BD=3,
∴OC=OA=$\sqrt{A{B}^{2}-O{B}^{2}}$=3$\sqrt{3}$,
∴AC=2OA=6$\sqrt{3}$,
∵点E在AC上,OE=$\sqrt{3}$,
∴当E在点O左边时CE=OC+$\sqrt{3}$=4$\sqrt{3}$
当点E在点O右边时CE=OC-$\sqrt{3}$=2$\sqrt{3}$,
∴CE=4$\sqrt{3}$或2$\sqrt{3}$;
故答案为:4$\sqrt{3}$或2$\sqrt{3}$.
点评 本题考查了菱形的性质、勾股定理、等边三角形的判定与性质;熟练掌握菱形的性质,由勾股定理求出OA是解决问题的关键.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
11.下列运算中,计算正确的是( )
| A. | (a2b)3=a5b3 | B. | (3a2)3=27a6 | C. | x6÷x2=x3 | D. | (a+b)2=a2+b2 |
8. 如图,⊙O中,弦AB、CD相交于点P,∠A=42°,∠APD=77°,则∠B的大小是( )
如图,⊙O中,弦AB、CD相交于点P,∠A=42°,∠APD=77°,则∠B的大小是( )
 如图,⊙O中,弦AB、CD相交于点P,∠A=42°,∠APD=77°,则∠B的大小是( )
如图,⊙O中,弦AB、CD相交于点P,∠A=42°,∠APD=77°,则∠B的大小是( )| A. | 43° | B. | 35° | C. | 34° | D. | 44° |
5.-2017的绝对值是( )
| A. | -2017 | B. | -$\frac{1}{2017}$ | C. | 2017 | D. | $\frac{1}{2017}$ |
9.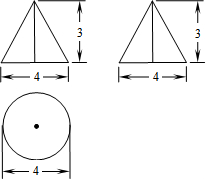 如图是一个几何体的三视图,则该几何体的侧面积是( )
如图是一个几何体的三视图,则该几何体的侧面积是( )
 如图是一个几何体的三视图,则该几何体的侧面积是( )
如图是一个几何体的三视图,则该几何体的侧面积是( )| A. | $2\sqrt{13}π$ | B. | 10π | C. | 20π | D. | $4\sqrt{13}π$ |