题目内容
12.矩形ABCD的对角线AC,BD相交于点O,请你添加一个适当的条件AB=BC(答案不唯一),使其成为正方形(只填一个即可)分析 此题是一道开放型的题目答案不唯一,证出四边形ABCD是菱形,由正方形的判定方法即可得出结论.
解答 解:添加条件:AB=BC,理由如下:
∵四边形ABCD是矩形,AB=BC,∴四边形ABCD是菱形,
∴四边形ABCD是正方形,
故答案为:AB=BC(答案不唯一).
点评 本题考查了矩形的性质,菱形的判定,正方形的判定的应用,能熟记正方形的判定定理是解此题的关键,注意:有一组邻边相等的矩形是正方形,对角线互相垂直的矩形是正方形.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
3.下列运算正确的是( )
| A. | a6÷a3=a2 | B. | 2a3+3a3=5a6 | C. | (-a3)2=a6 | D. | (a+b)2=a2+b2 |
7.下列算式运算结果正确的是( )
| A. | (2x5)2=2x10 | B. | (-3)-2=$\frac{1}{9}$ | C. | (a+1)2=a2+1 | D. | a-(a-b)=-b |
4.下列运算正确的是( )
| A. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | B. | ${({-\frac{1}{2}x{y^2}})^3}=-\frac{1}{6}{x^3}{y^6}$ | ||
| C. | (-x)5÷(-x)2=x3 | D. | $\sqrt{18}+\root{3}{-64}=3\sqrt{2}-4$ |
2.已知圆锥的底面面积为9πcm2,母线长为6cm,则圆锥的侧面积是( )
| A. | 18πcm2 | B. | 27πcm2 | C. | 18cm2 | D. | 27cm2 |
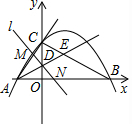 如图,已知抛物线y=ax2-2$\sqrt{3}$ax-9a与坐标轴交于A,B,C三点,其中C(0,3),∠BAC的平分线AE交y轴于点D,交BC于点E,过点D的直线l与射线AC,AB分别交于点M,N.
如图,已知抛物线y=ax2-2$\sqrt{3}$ax-9a与坐标轴交于A,B,C三点,其中C(0,3),∠BAC的平分线AE交y轴于点D,交BC于点E,过点D的直线l与射线AC,AB分别交于点M,N.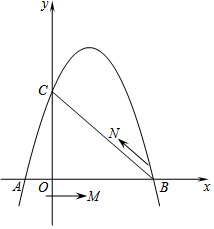 如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交于A、B两点,与y轴交于点C,且OA=2,OB=8,OC=6.
如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交于A、B两点,与y轴交于点C,且OA=2,OB=8,OC=6.