题目内容
14.已知圆锥底面半径是3,母线长是5,则圆锥的高是4,侧面积是15π,侧面展开所得扇形圆心角是216度.分析 根据勾股定理求得圆锥的高,圆锥的侧面积=底面周长×母线长÷2,把相应数值代入即可求解,根据弧长公式求出圆心角.
解答 解:圆锥的高=$\sqrt{{5}^{2}-{3}^{2}}$=4,
圆锥的侧面积=2π×3×5÷2=15π,
圆锥的底面周长=2π×3=6π;
扇形圆心角=$\frac{180×6π}{π×5}$=216°.
故答案为:4;15π;216.
点评 本题考查了圆锥的计算,解题的关键是弄清圆锥的侧面积的计算方法,特别是圆锥的底面周长等于圆锥的侧面扇形的弧长.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
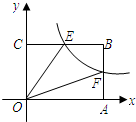 如图.矩形OABC的边OA,OC在坐标轴上,顶点B在第一象限,反比例函数y=$\frac{k}{x}$(k≠0)的图象经过AB的中点F,交BC于点E,且四边形OEBF的面积为2.求k的值.
如图.矩形OABC的边OA,OC在坐标轴上,顶点B在第一象限,反比例函数y=$\frac{k}{x}$(k≠0)的图象经过AB的中点F,交BC于点E,且四边形OEBF的面积为2.求k的值. 实数a、b在数轴上的位置如图所示,化简|a|+|b|-|a+b|.
实数a、b在数轴上的位置如图所示,化简|a|+|b|-|a+b|. 某型号的飞机的机翼形状如图所示,其中AB∥CD,请你根据图中的数据计算AC、BD和CD的长度(单位:米.结果保留根号).
某型号的飞机的机翼形状如图所示,其中AB∥CD,请你根据图中的数据计算AC、BD和CD的长度(单位:米.结果保留根号).