题目内容
19.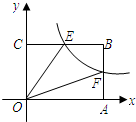 如图.矩形OABC的边OA,OC在坐标轴上,顶点B在第一象限,反比例函数y=$\frac{k}{x}$(k≠0)的图象经过AB的中点F,交BC于点E,且四边形OEBF的面积为2.求k的值.
如图.矩形OABC的边OA,OC在坐标轴上,顶点B在第一象限,反比例函数y=$\frac{k}{x}$(k≠0)的图象经过AB的中点F,交BC于点E,且四边形OEBF的面积为2.求k的值.
分析 设B点坐标为(a,b),由矩形OABC的边AB的中点为F,则F点的坐标为(a,$\frac{b}{2}$),根据反比例函数y=$\frac{k}{x}$(k≠0)系数k的几何意义得到S△OAF=S△OEC=$\frac{1}{2}$|k|=$\frac{1}{2}$a•$\frac{b}{2}$,则ab=2k,然后利用S矩形=S四边形OEBF+S△OAF+S△OEC得到ab=2+$\frac{1}{2}$k+$\frac{1}{2}$k,所以2k=k+2,再解一次方程即可.
解答 解:设B点坐标为(a,b),
∵矩形OABC的边AB的中点为F,
∴F点的坐标为(a,$\frac{b}{2}$),
∴S△OAF=S△OEC=$\frac{1}{2}$|k|=$\frac{1}{2}$a•$\frac{b}{2}$,
∴ab=2k,
∵S矩形=S四边形OEBF+S△OAF+S△OEC,
∴ab=2+$\frac{1}{2}$k+$\frac{1}{2}$k,
∴2k=k+2,
∴k=2.
点评 本题考查了反比例函数y=$\frac{k}{x}$(k≠0)系数k的几何意义:从反比例函数y=kx(k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|.

练习册系列答案
相关题目
9.将一些数排列查过下表:
观察规律后完成下列问题:
(1)第10行第2列的数是40;
(2)数81在9行1列;
(3)第n行第1列的数是n2;
(4)请写出数100所在的行和列.
| 第1列 | 第2列 | 第3列 | 第4列 | |
| 第1行 | 1 | 4 | 5 | 10 |
| 第2行 | 4 | 8 | 10 | 12 |
| 第3行 | 9 | 12 | 15 | 14 |
| … | … | … | … | … |
(1)第10行第2列的数是40;
(2)数81在9行1列;
(3)第n行第1列的数是n2;
(4)请写出数100所在的行和列.
8.两种移动电话计费式表:
(1)根据题意,一个月内在本地通话时间如下,请填下表
(2)当通话时间是多少时,使用两种移动电话费用一样?
(3)什么情况下,使用神州行?什么情况下,使用全球通?
| 全球通 | 神州行 | |
| 月租费 | 50元/月 | 0 |
| 本地通话费 | 0.40元/分 | 0.60元/分 |
| 时间(分) | 80 | 120 | x |
| 全球通费用 | 82 | 98 | 50+0.4x |
| 神州行费用 | 48 | 72 | 0.6x |
(3)什么情况下,使用神州行?什么情况下,使用全球通?
 如图,半径为1m.圆心角为90°的扇形薄铁板围成一个圆锥筒,求这个圆锥的容积.
如图,半径为1m.圆心角为90°的扇形薄铁板围成一个圆锥筒,求这个圆锥的容积. 在图甲和图乙中,∠1,∠2与∠B,∠C的关系是∠1+∠2=∠B+∠C.
在图甲和图乙中,∠1,∠2与∠B,∠C的关系是∠1+∠2=∠B+∠C.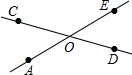 如图,反向延长OA得射线OE.
如图,反向延长OA得射线OE.