Question

15．如图，在△ABC中，D，E分别是AB，AC的中点，BE=2DE，延长DE到点F，使得EF=BE，连结CF．
（1）求证：四边形BCFE是菱形；
（2）若CE=4，∠BCF=120°，求AB的长．

Answer 1

分析 （1）由中位线定理，说明EF、BC平行，由边间关系2DE=BC、BE=2DE，说明EF、BC相等，先证明四边形BCFE是平行四边形，再证明四边形BCFE是菱形；
（2）由四边形BCFE是菱形，∠BCF=120°，说明∠ACB=60°，由AE=EC=BC=BE，得到∠A=30°，求出∠ABC的度数，在RT△ABC中，求出AB的长．

解答 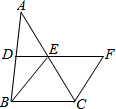（1）证明：∵D，E分别是AB，AC的中点，
∴DE∥BC，2DE=BC，
又∵BE=2DE，EF=BE，
∴EF=BC=BE，
∴四边形BCFE是菱形．
（2）解：∵四边形BCFE是菱形，∠BCF=120°，
∴∠ACB=60°，
∵BC=BE，
∴△BEC是等边三角形，
∴∠BEC=60°，
∵E是AC的中点，CE=4，
∴AE=EC=BE=4，∴∠A=30°，
∴∠ABC=180°-∠ACB-∠A=90°．
在Rt△ABC中，AB=$\sqrt{A{C}^{2}-B{C}^{2}}=\sqrt{{8}^{2}-{4}^{2}}=4\sqrt{3}$．

点评 本题考查了三角形的中位线定理、菱形的性质和判定及勾股定理．通过中位线定理把EF与BC连接起来是解决本题的关键．