题目内容
14.某运动器械厂根据市场需求,计算生产A、B两种型号的按摩椅,某部分信息如下:A、B两种型号的按摩椅共生产40台,该厂所筹生产按摩椅的资金不少于90万元,但不超过91万元,且所筹资金全部用于这两种按摩椅,现已知A、B两种按摩椅的生产成本和售价如表:| 型号 | 成本(万元/台) | 售价(万元/台) |
| A | 2 | 2.4 |
| B | 2.5 | 3 |
(1)该公司对此两种按摩椅有几种生产方案?那种生产方案获得最大利润?
(2)据市场调查,每台A型按摩椅的售价将会提高a万元(a>0),每台B型按摩椅售价不会改变,该公司应如何生产才可以获得最大利润?
分析 (1)在题目中,每种型号的成本及总成本的上限和下限都已知,所以设生产A型按摩椅x台,则B型按摩椅(40-x)台的情况下,可列不等式组得:$\left\{\begin{array}{l}{2x+2.5(40-x)≥90}\\{2x+2.5(40-x)≤91}\end{array}\right.$,解不等式组,取其整数值即可求解;在知道生产方案以及每种利润情况下可列函数解析式w=(2.4-2)x+(3-2.5)×(40-x)=20-0.1x,利用函数的自变量取值范围和其单调性即可求得函数的最值;
(2)结合(1)得,在此w′=(0.4+a)x+0.5(40-x)=(a-0.1)x+20,必须把(a-0.1)正负性考虑清楚,即a>0.1,a=0.1,a<0.1三种情况,最终才能得出结论,即怎样安排,完全取决于a的大小.
解答 解:(1)设生产A种型号的按摩椅x台,则B型按摩椅(40-x)台,生产利润为w万元,
有题意得:$\left\{\begin{array}{l}{2x+2.5(40-x)≥90}\\{2x+2.5(40-x)≤91}\end{array}\right.$,
解得:18≤x≤20,
∵x取非负整数,
∴x为18,19,20.
∴有三种生产方案
①A型按摩椅18台,B型按摩椅22台;
②A型按摩椅19台,B型按摩椅21台;
③A型按摩椅20台,B型按摩椅20台;
w=(2.4-2)x+(3-2.5)×(40-x)=20-0.1x,
∵-0.1<0,
∴当x=18时,w最大=20-0.1×18=18.2,
∴该公司对此两种按摩椅有3种生产方案,当生产A型按摩椅18台,B型按摩椅22台;获得最大利润18.2万元.
(2)当每台A型按摩椅的售价将会提高a万元(a>0),每台B型按摩椅售价不会改变时,此时的利润为:
w′=(0.4+a)x+0.5(40-x)=(a-0.1)x+20,
当a-0.1>0时,即a>0.1,
∴当x=20时,w′最大=20a+18,
即当生产A型按摩椅20台,B型按摩椅20台,获得最大利润.
当a-0.1=0时,即a=0.1,
∴当x=20时,w′=20,
即三种生产方案的获利一样大.
当a-0.1<0时,即a<0.1,
∴当x=18时,w′最大=18a+18.2,
即当生产A型按摩椅18台,B型按摩椅22台,获得最大利润.
答:当a>0.1时,当生产A型按摩椅20台,B型按摩椅20台,获得最大利润;
当a=0.1时,3种方案获利一样;
当a<0.1时,生产A型按摩椅18台,B型按摩椅22台,获得最大利润.
点评 本题考查了一次函数的应用,考查学生解决实际问题的能力,解决本题的关键是用函数知识去解题,以及会讨论函数的最大值.要结合自变量的范围求函数的最大值,并要把(a-0.1)正负性考虑清楚,分情况讨论问题.

 阅读快车系列答案
阅读快车系列答案 如图,在正方形ABCD的外侧,作等边三角形ADE,连结BE交AD于点F,则∠DFE的度数为( )
如图,在正方形ABCD的外侧,作等边三角形ADE,连结BE交AD于点F,则∠DFE的度数为( )| A. | 45° | B. | 55° | C. | 60° | D. | 75° |
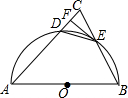 如图,在△ABC中,AB=AC,以AB为直径的半圆O与AC交于点D,与BC交于点E,连接DE,过点E作EF⊥AC,垂足为点F.
如图,在△ABC中,AB=AC,以AB为直径的半圆O与AC交于点D,与BC交于点E,连接DE,过点E作EF⊥AC,垂足为点F.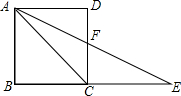 如图,正方形ABCD,AC=CE,则∠DAF=22.5°.
如图,正方形ABCD,AC=CE,则∠DAF=22.5°.
 如图所示
如图所示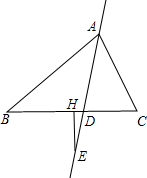 如图,在△ABC中,AD平分∠CAB,点E是直线AD上的动点(H点不与D点重合),过点E作BC的垂线段EH,探索∠DEH,∠B,∠C之间的关系.
如图,在△ABC中,AD平分∠CAB,点E是直线AD上的动点(H点不与D点重合),过点E作BC的垂线段EH,探索∠DEH,∠B,∠C之间的关系. 如图所示,直线AB,CD相交于点O,OM⊥AB,若∠MOD=30°,则∠COB=120度.
如图所示,直线AB,CD相交于点O,OM⊥AB,若∠MOD=30°,则∠COB=120度.