题目内容
4.一个直角三角形一条边为7,另一条边为13,求另一条边的长.分析 本题已知直角三角形的两边长,但未明确这两条边是直角边还是斜边,因此两条边中的较长边13既可以是直角边,也可以是斜边,所以求第三边的长必须分类讨论,即4是斜边或直角边的两种情况,然后利用勾股定理求解.
解答 解:设第三边为x,
(1)若13是直角边,则第三边x是斜边,由勾股定理得:
132+72=x2,
∴x=$\sqrt{218}$;
(2)若13是斜边,则第三边x为直角边,由勾股定理得:
72+x2=132,
∴x=2$\sqrt{30}$;
∴第三边的长为2$\sqrt{30}$或$\sqrt{218}$.
点评 本题考查了利用勾股定理解直角三角形的能力,当已知条件中没有明确哪是斜边时,要注意讨论,一些学生往往忽略这一点,造成丢解.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
13.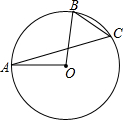 如图,点A,B,C是⊙O上的三点,已知∠AOB=100°,那么∠ACB的度数是( )
如图,点A,B,C是⊙O上的三点,已知∠AOB=100°,那么∠ACB的度数是( )
 如图,点A,B,C是⊙O上的三点,已知∠AOB=100°,那么∠ACB的度数是( )
如图,点A,B,C是⊙O上的三点,已知∠AOB=100°,那么∠ACB的度数是( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
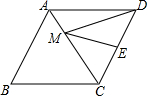 如图,菱形ABCD的边长为4,且∠ABC=60°,点E是CD的中点,点M为AC上一点,求MD+ME的最小值.
如图,菱形ABCD的边长为4,且∠ABC=60°,点E是CD的中点,点M为AC上一点,求MD+ME的最小值.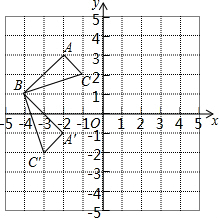 在平面直角坐标系中,△ABC的位置如图所示,网格中小正方形的边长为1,请回答下列问题:
在平面直角坐标系中,△ABC的位置如图所示,网格中小正方形的边长为1,请回答下列问题: