题目内容
12.在圆中,45°的圆周角所对的弦长为4$\sqrt{2}$,则圆的半径为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 根据圆周角定理,可得圆心角,根据勾股定理,可得半径.
解答 解:圆心角是90°,
由勾股定理,得
r2+r2=(4$\sqrt{2}$)2,
解得r=4,
故选:C.
点评 本题考查了圆周角定理,利用了同弦圆周角等于圆心角的一半得出圆心角是解题关键.

练习册系列答案
相关题目
20.对于反比例函数$y=\frac{k}{x}$,如果当-2≤x≤-1时有最大值y=4,则当x≥8时,有( )
| A. | 最小值y=$-\frac{1}{2}$ | B. | 最小值y=-1 | C. | 最大值y=$-\frac{1}{2}$ | D. | 最大值y=-1 |
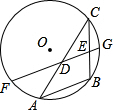 如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点D、E分别是AC、BC的中点,直线DE交⊙O于F、G两点.若⊙O的半径7,则FD+EG的最大值为10.5.
如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点D、E分别是AC、BC的中点,直线DE交⊙O于F、G两点.若⊙O的半径7,则FD+EG的最大值为10.5.