题目内容
解方程:x3+(4-a)x2+(2-2a)x+a2-2a-3=0.
考点:因式分解的应用
专题:
分析:原方程可以转化为:[x-(a-3)][x2+x-(a-1)]=0的形式,然后通过分类讨论求得x的值.
解答:解:∵x3+(4-a)x2+(2-2a)x+a2-2a-3
=x2(x+3+a)+[x-(a+1)][x-(a-3)]
=[x-(a-3)][x2+x-(a-1)],
∴由原方程得[x-(a-3)][x2+x-(a-1)]=0.
当a≥-
时,x1=a-3,x2=
,x3=
,
当a<-
时,x=a-3.
=x2(x+3+a)+[x-(a+1)][x-(a-3)]
=[x-(a-3)][x2+x-(a-1)],
∴由原方程得[x-(a-3)][x2+x-(a-1)]=0.
当a≥-
| 5 |
| 4 |
1+
| ||
| 2 |
1-
| ||
| 2 |
当a<-
| 5 |
| 4 |
点评:本题考查了高次方程,难度较大,关键是正确的利用提公因式进行合并后再计算.

练习册系列答案
相关题目
某电视台每播放18分钟节目便插播2分钟广告,打开电视收看该台恰好遇到广告的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 已知:如图,四边形ABCD中,∠B=∠D=90°,AE平分∠DAB,CF平分∠BCD.
已知:如图,四边形ABCD中,∠B=∠D=90°,AE平分∠DAB,CF平分∠BCD. 如图,等腰Rt△ABC的直角顶点B在直线PQ上,AD⊥PQ,CE⊥PQ,AD=2cm,DB=4cm,求S△BCE.
如图,等腰Rt△ABC的直角顶点B在直线PQ上,AD⊥PQ,CE⊥PQ,AD=2cm,DB=4cm,求S△BCE.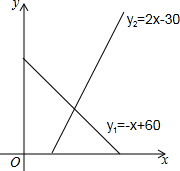 某地区一种商品的需求量y1(万件),供应量y2(万件)与价格x(元/件)分别近似满足下列函数关系式:y1=-x+60,y2=2x-30.需求量为0时,即停止供应.当y1=y2时,该商品的价格称为稳定价格,需求量称为稳定需求量.
某地区一种商品的需求量y1(万件),供应量y2(万件)与价格x(元/件)分别近似满足下列函数关系式:y1=-x+60,y2=2x-30.需求量为0时,即停止供应.当y1=y2时,该商品的价格称为稳定价格,需求量称为稳定需求量. 如图,a,b,c是数轴上三个点A、B、C所对应的实数.试化简:
如图,a,b,c是数轴上三个点A、B、C所对应的实数.试化简: