题目内容
 如图,等腰Rt△ABC的直角顶点B在直线PQ上,AD⊥PQ,CE⊥PQ,AD=2cm,DB=4cm,求S△BCE.
如图,等腰Rt△ABC的直角顶点B在直线PQ上,AD⊥PQ,CE⊥PQ,AD=2cm,DB=4cm,求S△BCE.考点:全等三角形的判定与性质
专题:
分析:根据同角的余角相等求出∠ABD=∠BCE,再利用“角角边”证明△ABD和△BCE全等,根据全等三角形对应边相等可得BE=AD,CE=BD,然后利用三角形的面积公式列式计算即可得解.
解答:解:∵∠ABC=90°,
∴∠ABD+∠CBE=90°,
∵AD⊥PQ,CE⊥PQ,
∴∠ADB=∠BEC=90°,
∠BCE+∠CBE=90°,
∴∠ABD=∠BCE,
在△ABD和△BCE中,
,
∴△ABD≌△BCE(AAS),
∴BE=AD=2cm,CE=BD=4cm,
∴S△BCE=
BE•CE=
×2×4=4cm2.
∴∠ABD+∠CBE=90°,
∵AD⊥PQ,CE⊥PQ,
∴∠ADB=∠BEC=90°,
∠BCE+∠CBE=90°,
∴∠ABD=∠BCE,
在△ABD和△BCE中,
|
∴△ABD≌△BCE(AAS),
∴BE=AD=2cm,CE=BD=4cm,
∴S△BCE=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了全等三角形的判定与性质,同角的余角相等的性质,三角形的面积,熟练掌握全等三角形的判定方法并确定出全等三角形是解题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
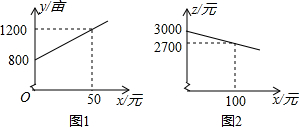 某市种植某种绿色蔬菜,全部用来出口.为了扩大出口规模,该市决定对这种蔬菜的种植实行政府补贴,规定每种植一亩这种蔬菜一次性补贴菜农若干元.经调查,种植亩数y(亩)与补贴数额x(元)之间大致满足如图1所示的一次函数关系.随着补贴数额x的不断增大,出口量也不断增加,但每亩蔬菜的收益z(元)会相应降低,且z与x之间也大致满足如图2所示的一次函数关系.
某市种植某种绿色蔬菜,全部用来出口.为了扩大出口规模,该市决定对这种蔬菜的种植实行政府补贴,规定每种植一亩这种蔬菜一次性补贴菜农若干元.经调查,种植亩数y(亩)与补贴数额x(元)之间大致满足如图1所示的一次函数关系.随着补贴数额x的不断增大,出口量也不断增加,但每亩蔬菜的收益z(元)会相应降低,且z与x之间也大致满足如图2所示的一次函数关系. 如图,AD是△ABC的中线,P为AD上任意一点,连接BP并延长,交AC于F,连接CP并延长,交AB于E,连接EF.求证:EF∥BC.
如图,AD是△ABC的中线,P为AD上任意一点,连接BP并延长,交AC于F,连接CP并延长,交AB于E,连接EF.求证:EF∥BC.