题目内容
10.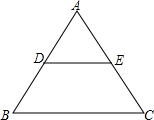 如图,边长为4的等边△ABC中,DE为中位线,则四边形BCED的周长为10.
如图,边长为4的等边△ABC中,DE为中位线,则四边形BCED的周长为10.
分析 根据三角形中位线定理求出DE的长,根据四边形BCED的周长=BC+CE+ED+DB,代入计算得到答案.
解答 解:∵AB=AC=BC=4,DE为中位线,
∴BD=$\frac{1}{2}$AB=2,EC=$\frac{1}{2}$AC=2,DE=$\frac{1}{2}$BC=2,
∴四边形BCED的周长=BC+CE+ED+DB=10,
故答案为:10.
点评 本题考查的是三角形中位线定理,掌握三角形的中位线平行于第三边且等于第三边的一半是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.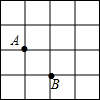 如图,A、B是边长为1的小正方形组成的网格上的两个格点,在格点中任意放置点C,恰好能使△ABC的面积为1的概率是( )
如图,A、B是边长为1的小正方形组成的网格上的两个格点,在格点中任意放置点C,恰好能使△ABC的面积为1的概率是( )
 如图,A、B是边长为1的小正方形组成的网格上的两个格点,在格点中任意放置点C,恰好能使△ABC的面积为1的概率是( )
如图,A、B是边长为1的小正方形组成的网格上的两个格点,在格点中任意放置点C,恰好能使△ABC的面积为1的概率是( )| A. | $\frac{6}{25}$ | B. | $\frac{1}{5}$ | C. | $\frac{4}{25}$ | D. | $\frac{7}{25}$ |
19.已知某同学近几次的数学成绩(单位:分)分别为92,90,88,92,93,则该同学这几次数学成绩的平均数和众数分别是( )
| A. | 90分,90分 | B. | 91分,92分 | C. | 92分,92分 | D. | 89分,92分 |

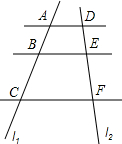 如图,已知AD∥BE∥CF,若$\frac{AB}{BC}=\frac{2}{5}$,求$\frac{DE}{EF}$的值.
如图,已知AD∥BE∥CF,若$\frac{AB}{BC}=\frac{2}{5}$,求$\frac{DE}{EF}$的值.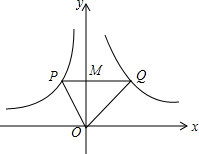 如图,点P(-1,2)、Q(2,2)分别位于两个不同的双曲线上,则S△POQ=3.
如图,点P(-1,2)、Q(2,2)分别位于两个不同的双曲线上,则S△POQ=3. 已知二次函数y=-x2+mx-3.
已知二次函数y=-x2+mx-3.