题目内容
1.在△ABC中,AB=5,AC=10,∠A=40°,在△DEF中,DE=6,DF=12,填上一个合适的条件∠D=40°,能使△ABC∽△DEF.分析 利用AB=5,AC=10,DE=6,DF=12可计算出$\frac{AB}{DE}$=$\frac{AC}{DF}$=$\frac{5}{6}$,根据两组对应边的比相等且夹角对应相等的两个三角形相似,则当∠A=∠D时,△ABC∽△DEF,所以添加∠D=40°.
解答 解:∵AB=5,AC=10,DE=6,DF=12,
∴$\frac{AB}{DE}$=$\frac{AC}{DF}$=$\frac{5}{6}$,
∴当∠A=∠D时,△ABC∽△DEF,
而∠A=40°,
∴当添加∠D=40°时,可判断△ABC∽△DEF.
故答案为∠D=40°.
点评 本题考查了相似三角形的判定:两组对应边的比相等且夹角对应相等的两个三角形相似.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
11.下表是某批足球质量检验获得的数据,请根据此表回答,当抽取的足球数很大时,这批足球优等品的频率会在常数0.95附近摆动.
| 抽取的足球数 | 50 | 100 | 200 | 500 | 1000 | 2000 |
| 优等品数 | 47 | 95 | 194 | 472 | 953 | 1902 |
 如图,AB,CD为⊙O的两条直径,E,F分别为OA,OB的中点,求证:四边形CEDF为平行四边形.
如图,AB,CD为⊙O的两条直径,E,F分别为OA,OB的中点,求证:四边形CEDF为平行四边形.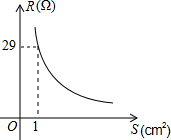 实验表明,当导线的长度一定时,导线的电阻与它的横截面积成反比例,一条长为100km的铅导线的电阻R(Ω)与它的横截面积S(cm2)的函数图象如图所示,那么,其函数关系式为R=$\frac{29}{S}$;当S=2cm2时,R=14.5Ω.
实验表明,当导线的长度一定时,导线的电阻与它的横截面积成反比例,一条长为100km的铅导线的电阻R(Ω)与它的横截面积S(cm2)的函数图象如图所示,那么,其函数关系式为R=$\frac{29}{S}$;当S=2cm2时,R=14.5Ω.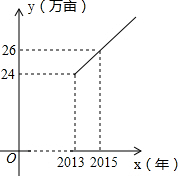 某市实施“农业立市,工业强市,旅游兴市”计划后,2013年全市荔枝种植面积为24万亩.调查分析结果显示:从2013年开始,该市荔枝种植面积y(万亩)随着时间x(年)逐年成直线上升,y与x之间的函数关系如图所示.
某市实施“农业立市,工业强市,旅游兴市”计划后,2013年全市荔枝种植面积为24万亩.调查分析结果显示:从2013年开始,该市荔枝种植面积y(万亩)随着时间x(年)逐年成直线上升,y与x之间的函数关系如图所示. 如图.D点是△ABC的AC边的延长线上一点,E是BC上一点,连接DE.求证:∠BED>∠A.
如图.D点是△ABC的AC边的延长线上一点,E是BC上一点,连接DE.求证:∠BED>∠A.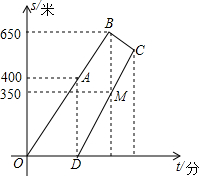 小明要在周日8点50分之前赶到距家1000米的书店去买书.早8点20分从家出发,8分钟后妈妈发现他忘了带钱包,于是立即出发按他走的路线去追.妈妈出发几分钟后,小明也发现了忘带钱包,于是按原路原速返回去取,几分钟后与妈妈相遇.假设在此过程中小明和妈妈的速度均保持不变,如图所示,给出两人离家距离s(米)和小明所走的时间t(分)之间的函数图象,结合图象回答下列问题:
小明要在周日8点50分之前赶到距家1000米的书店去买书.早8点20分从家出发,8分钟后妈妈发现他忘了带钱包,于是立即出发按他走的路线去追.妈妈出发几分钟后,小明也发现了忘带钱包,于是按原路原速返回去取,几分钟后与妈妈相遇.假设在此过程中小明和妈妈的速度均保持不变,如图所示,给出两人离家距离s(米)和小明所走的时间t(分)之间的函数图象,结合图象回答下列问题: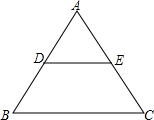 如图,边长为4的等边△ABC中,DE为中位线,则四边形BCED的周长为10.
如图,边长为4的等边△ABC中,DE为中位线,则四边形BCED的周长为10.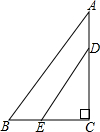 已知,在Rt△ABC中,∠C=90°,DE∥AB,AD=$\frac{1}{4}$AC,若CD=3,BE=$\frac{3}{4}$,求AB的长.
已知,在Rt△ABC中,∠C=90°,DE∥AB,AD=$\frac{1}{4}$AC,若CD=3,BE=$\frac{3}{4}$,求AB的长.