题目内容
 如图,四边形ABCD中,AB∥CD,CE∥AD交AB于E,AE=AD.
如图,四边形ABCD中,AB∥CD,CE∥AD交AB于E,AE=AD.(1)求证:四边形AECD是菱形;
(2)若∠ACB=90°,点E是AB的中点,BC=6,AC=8,求菱形AECD的面积.
考点:菱形的判定与性质,勾股定理
专题:
分析:(1)首先根据定义证明四边形AECD是平行四边形,则以及菱形的定义即可证得;
(2)首先求得△ABC的面积,则△ACE的面积即可求得,根据S菱形AECD=2S△ACE即可求解.
(2)首先求得△ABC的面积,则△ACE的面积即可求得,根据S菱形AECD=2S△ACE即可求解.
解答:证明:(1)∵AB∥CD,CE∥AD,
∴四边形AECD是平行四边形,
∵AE=AD,
∴四边形AECD是菱形;
(2)在RtABC中S△ABC=
×6×8=24,
∵点E是AB的中点,
∴S△ACE=
S△ABC=
×24=12,
∴S菱形AECD=2S△ACE=2×12=24.
∴四边形AECD是平行四边形,
∵AE=AD,
∴四边形AECD是菱形;
(2)在RtABC中S△ABC=
| 1 |
| 2 |
∵点E是AB的中点,
∴S△ACE=
| 1 |
| 2 |
| 1 |
| 2 |
∴S菱形AECD=2S△ACE=2×12=24.
点评:本题考查了菱形的定义以及三角形的面积、菱形的面积的计算,理解S菱形AECD=2S△ACE是关键.

练习册系列答案
相关题目
下列结论正确的是( )
| A、a2b3c是五次单项式 |
| B、xyz的系数是0 |
| C、x5+3x2y4-27是六次三项式 |
| D、3x2-x+1的一次项系数是1 |
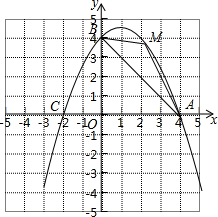 如图,在平面直角坐标系中,已知抛物线经过点A(4,0),B(0,4),C(-2,0)三点.
如图,在平面直角坐标系中,已知抛物线经过点A(4,0),B(0,4),C(-2,0)三点.  已知:如图所示,△ABC中,E、F、D分别是AB、AC、BC上的点,且DE∥AC,DF∥AB,AD平分∠BAC,求证:四边形AEDF是菱形.
已知:如图所示,△ABC中,E、F、D分别是AB、AC、BC上的点,且DE∥AC,DF∥AB,AD平分∠BAC,求证:四边形AEDF是菱形.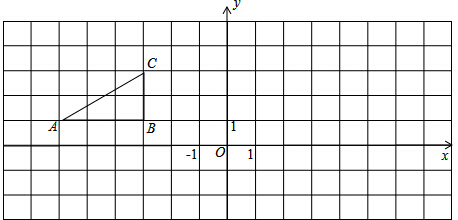
 尺规作图:
尺规作图: