题目内容
 如图,在三角形ABC中,BE平分∠ABC,∠1=∠2,∠C=70°,求∠AED的度数.
如图,在三角形ABC中,BE平分∠ABC,∠1=∠2,∠C=70°,求∠AED的度数.考点:平行线的判定与性质
专题:
分析:根据角平分线定义求出∠1=∠CBE,求出∠2=∠CBE,根据平行线的判定得出DE∥BC,根据平行线的性质得出∠AED=∠C,代入求出即可.
解答:解:∵BE平分∠ABC,
∴∠1=∠CBE,
∵∠1=∠2,
∴∠2=∠CBE,
∴DE∥BC,
∵∠C=70°,
∴∠AED=∠C=70°.
∴∠1=∠CBE,
∵∠1=∠2,
∴∠2=∠CBE,
∴DE∥BC,
∵∠C=70°,
∴∠AED=∠C=70°.
点评:本题考查了平行线的性质和判定,角平分线定义的应用,能运用平行线的性质和判定进行推理是解此题的关键,注意:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,反之亦然.

练习册系列答案
相关题目
 如图,直线l对应的函数表达式是( )
如图,直线l对应的函数表达式是( )| A、y=x+1 |
| B、y=-x+1 |
| C、y=x-1 |
| D、y=-x-1 |
 如图,点F在直线AB上,已知∠1和∠D互余,CF⊥DF.求证:AB∥CD.
如图,点F在直线AB上,已知∠1和∠D互余,CF⊥DF.求证:AB∥CD.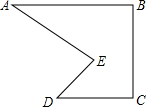 小明到工厂去进行社会实践活动,发现工人师傅生产了一种如图所示的零件,要求AB∥CD,∠BAE=30°.∠AED=70°.小明发现工人师傅只是量出∠BAE=30°.∠AED=70°后,又量了∠EDC=40°,就说AB与CD肯定是平行的,你知道是什么原因吗?
小明到工厂去进行社会实践活动,发现工人师傅生产了一种如图所示的零件,要求AB∥CD,∠BAE=30°.∠AED=70°.小明发现工人师傅只是量出∠BAE=30°.∠AED=70°后,又量了∠EDC=40°,就说AB与CD肯定是平行的,你知道是什么原因吗? 如图,如果半径为1个单位长度的圆上有一点A,且点A与数轴上表示5.1的点重合(圆与数轴只有这一个交点),让圆沿数轴的负方向滚动一周,点A到达另一点B,则A,B两点之间表示整数的点共有( )
如图,如果半径为1个单位长度的圆上有一点A,且点A与数轴上表示5.1的点重合(圆与数轴只有这一个交点),让圆沿数轴的负方向滚动一周,点A到达另一点B,则A,B两点之间表示整数的点共有( ) 如图,在?ABCD中,平行于AB的直线交BC于点P,交AD于点Q,M为AP、BQ的交点,N为DP、CQ的交点,猜想MN与AD的关系并说明理由.
如图,在?ABCD中,平行于AB的直线交BC于点P,交AD于点Q,M为AP、BQ的交点,N为DP、CQ的交点,猜想MN与AD的关系并说明理由. 如图,
如图, 如图,延长△ABC的中线BD至E,使∠DAE=∠BCA.四边形ABCE是平行四边形吗?你找到了几种证法?
如图,延长△ABC的中线BD至E,使∠DAE=∠BCA.四边形ABCE是平行四边形吗?你找到了几种证法? 如图,某公路上A,B两点的正南方有D,C两村庄,现要在公路AB上建一个车站E,使C,D两村到E站的距离相等,已知AB=50km,DA=20km,CB=10km,请你设计出E站的位置,并计算车站E距A点多远?
如图,某公路上A,B两点的正南方有D,C两村庄,现要在公路AB上建一个车站E,使C,D两村到E站的距离相等,已知AB=50km,DA=20km,CB=10km,请你设计出E站的位置,并计算车站E距A点多远?