题目内容
4.已知一次函数y=x-2与二次函数y=x2+kx+k(1)若两个函数图象交点的横坐标的平方和等于9,求二次函数解析式.
(2)若二次函数图象与x轴的两个交点位于一次函数图象与x轴交点的两侧,求k的取值范围.
(3)k能否取值,使y轴右侧的抛物线总在直线的下方?若能够,求出k的取值范围;若不能,试说明理由.
分析 (1)先将函数问题转化出一元二次方程问题,利用一元二次方程根的判别式和根与系数的关系即可;
(2)先确定出直线和x轴的交点坐标,由题意直接得出,当x=2时,函数值小于0,即可求出k的范围;
(3)先由抛物线的a值是1是一个定值,并且大于1,得出抛物线开口向上,即有抛物线向上无限延伸,即可得出结论.
解答 解:(1)∵一次函数y=x-2①与二次函数y=x2+kx+k②,
∴联立①②得,x2+(k-1)x+k+2=0,
∴x1+x2=1-k,x1x2=k+2,
∵两个函数图象交点的横坐标的平方和等于9
∴△=(k-1)2-4(k+2)>0,
∴k>7或k<-1,
∵x12+x22=(x1+x2)2-2x1x2=(1-k)2-2(k+2)=9,
∴k=6(舍)或k=-2,
∴二次函数的解析式为y=x2-2x-2,
(2)∵一次函数y=x-2,
∴直线和x轴的交点坐标为(2,0)
由(1)知,二次函数的解析式为y=x2-2x-2,
∴抛物线开口向上,
∵二次函数图象与x轴的两个交点位于一次函数图象与x轴交点的两侧
∴当x=2时,二次函数值22+2k+k<0,
∴k<-$\frac{4}{3}$;
(3)不存在,
理由:∵抛物线解析式为y=x2+kx+k,
∴a=1>0,
∴抛物线开口方向向上,
即:抛物线两头向上无限延伸,
∴抛物线要么全部在某直线上方,要么被直线分成两部分,不可能总在直线下方.
故不存在实数k,使抛物线在y轴右侧的部分总在直线y=x-2的下方.
点评 此题是二次函数综合题,主要考查了函数转化成一元二次方程的方法,一元二次方程的根的判别式,根与系数的关系,解本题的关键是将函数问题转化成一元二次方程的问题.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
14.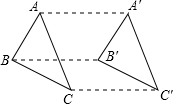 如图,△ABC沿着AA′方向平移到△A′B′C′,下列说法正确的是( )
如图,△ABC沿着AA′方向平移到△A′B′C′,下列说法正确的是( )
 如图,△ABC沿着AA′方向平移到△A′B′C′,下列说法正确的是( )
如图,△ABC沿着AA′方向平移到△A′B′C′,下列说法正确的是( )| A. | AB与A′B′平行但不相等 | B. | AB与A′B′相等但不平行 | ||
| C. | AB与A′B′平行且相等 | D. | 无法确定AB与A′B′的关系 |
15.小明用配方法解下列方程时,只有一个配方有错误,则小明配方正确的是( )
| A. | x2-2x-79=0化成(x-1)2=80 | B. | x2+x+9=0化成(x+4)2=25 | ||
| C. | 4t2-7t-8=0化成(t-$\frac{7}{8}$)2=$\frac{177}{64}$ | D. | 3y2-8y-2=0化成(y-$\frac{4}{3}$)2=$\frac{22}{9}$ |
12.-(+2)的相反数是( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | -2 |
16.下列计算结果正确的是( )
| A. | -3.5÷$\frac{7}{8}$×($-\frac{3}{4}$)=-3 | B. | -2÷3×3=-$\frac{2}{9}$ | C. | (-6)÷(-4)÷(+$\frac{6}{5}$)=$\frac{5}{4}$ | D. | -$\frac{1}{30}$÷($\frac{1}{6}$÷$\frac{1}{5}$)=-1 |
13. 如图,在△ABC中,AB=AC,∠A=70°,∠OBC=∠OCA,则∠BOC的度数为( )
如图,在△ABC中,AB=AC,∠A=70°,∠OBC=∠OCA,则∠BOC的度数为( )
 如图,在△ABC中,AB=AC,∠A=70°,∠OBC=∠OCA,则∠BOC的度数为( )
如图,在△ABC中,AB=AC,∠A=70°,∠OBC=∠OCA,则∠BOC的度数为( )| A. | 140° | B. | 110° | C. | 125° | D. | 115° |
15. 如图,平行四边形ABCD中,对角线AC,BD相交于O,AC=8,BD=10,则边AB的取值范围是( )
如图,平行四边形ABCD中,对角线AC,BD相交于O,AC=8,BD=10,则边AB的取值范围是( )
 如图,平行四边形ABCD中,对角线AC,BD相交于O,AC=8,BD=10,则边AB的取值范围是( )
如图,平行四边形ABCD中,对角线AC,BD相交于O,AC=8,BD=10,则边AB的取值范围是( )| A. | 8<AB<10 | B. | 1<AB<9 | C. | 4<AB<5 | D. | 2<AB<18 |
 如图,$\frac{AD}{AC}$=$\frac{DE}{AB}$=$\frac{AE}{BC}$,求证:AB=AE.
如图,$\frac{AD}{AC}$=$\frac{DE}{AB}$=$\frac{AE}{BC}$,求证:AB=AE.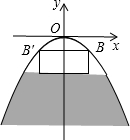 某河上由抛物线形拱桥,当水面距拱顶5m时,水面宽8m,一木船宽4m,高2m,载货后,木船露出水面的部分为$\frac{3}{4}$m,问:水面涨到与抛物线拱顶相距多少米时,木船开始不能通航?
某河上由抛物线形拱桥,当水面距拱顶5m时,水面宽8m,一木船宽4m,高2m,载货后,木船露出水面的部分为$\frac{3}{4}$m,问:水面涨到与抛物线拱顶相距多少米时,木船开始不能通航?