题目内容
16. 《九章算术》卷九“勾股”中记载:今有户不知高广,竿不知长短,横之不出四尺,纵之不出二尺,斜之适出,问户斜几何.
《九章算术》卷九“勾股”中记载:今有户不知高广,竿不知长短,横之不出四尺,纵之不出二尺,斜之适出,问户斜几何.注:横放,竿比门宽长出四尺;竖放,竿比门高长出二尺,斜放恰好能出去.
解决下列问题:
(1)示意图中,线段CE的长为4尺,线段DF的长为2尺;
(2)求户斜多长.
分析 (1)根据题意直接填空即可;
(2)根据题中所给的条件可知,竿斜放就恰好等于门的对角线长,可与门的宽和高构成直角三角形,运用勾股定理可求出门对角线长.
解答 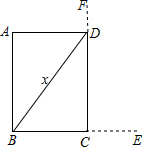 解:(1)由“横放,竿比门宽长出四尺”可得CE=4尺,
解:(1)由“横放,竿比门宽长出四尺”可得CE=4尺,
由“竖放,竿比门高长出二尺”可得DE=2尺,
故答案是:4;2;
(2)设户斜x尺,则图中BD=x.
BC=BE-CE=x-4(x>4)
CD=CF-DF=x-2(x>2)
又在直角三角形BCD中,∠BCD=90°,
由勾股定理得:BC2+CD2=BD2,
所以(x+4)2+(x-2)2=x2,
整理,得x2-12x+20=0,
因式分解,得(x-10)(x-2)=0,
解得x1=10,x2=2
因为x>4且x>2,
所以x=2舍去,x=10.
答:户斜为10尺.
点评 本题考查勾股定理的运用,正确运用勾股定理,将数学思想运用到实际问题中是解答本题的关键,难度一般.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
 如图所示,点E在CA的延长线上,AD⊥BC于点D,EF⊥BC于点F,∠E=∠1,试说明AD平分∠BAC的理由.
如图所示,点E在CA的延长线上,AD⊥BC于点D,EF⊥BC于点F,∠E=∠1,试说明AD平分∠BAC的理由. 已知:如图,BE∥CD,∠A=∠1.求证:∠C=∠E.
已知:如图,BE∥CD,∠A=∠1.求证:∠C=∠E. 设△ABC中,∠BAC=60°,∠ATC=∠BTC=∠BTA=120°,点M是BC的中点.求证:TA+TB+TC=2AM.
设△ABC中,∠BAC=60°,∠ATC=∠BTC=∠BTA=120°,点M是BC的中点.求证:TA+TB+TC=2AM. 如图,在△ABC中,D是BC边上的一点,已知AB=13,AD=12,AC=15,BD=5.
如图,在△ABC中,D是BC边上的一点,已知AB=13,AD=12,AC=15,BD=5. 如图,在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=5,DA=5$\sqrt{2}$,则BD的长为$\sqrt{65}$.
如图,在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=5,DA=5$\sqrt{2}$,则BD的长为$\sqrt{65}$.