题目内容
8.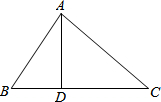 如图,在△ABC中,D是BC边上的一点,已知AB=13,AD=12,AC=15,BD=5.
如图,在△ABC中,D是BC边上的一点,已知AB=13,AD=12,AC=15,BD=5.(1)求证:AD⊥BC;
(2)求CD的长.
分析 (1)根据勾股定理逆定理可得AD2+BD2=AB2,即可得证;
(2)由勾股定理知AD2+CD2=AC2,即122+CD2=152,解之可得答案.
解答 解:(1)在△ABD中,
∵AD2+BD2=122+52=169,AB2=132=169,
∴AD2+BD2=AB2,
∴△ABD是直角三角形,其中∠ADB=90°,
∴AD⊥BC;
(2)∵AD⊥BC,
∴∠ADC=90°,
在Rt△ACD中,AD2+CD2=AC2,
即122+CD2=152,解得:CD=9或CD=-9(舍).
点评 本题主要考查勾股定理及其逆定理,熟练掌握勾股定理及其逆定理是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
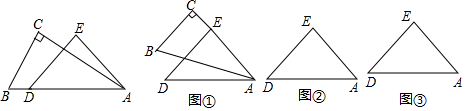
 《九章算术》卷九“勾股”中记载:今有户不知高广,竿不知长短,横之不出四尺,纵之不出二尺,斜之适出,问户斜几何.
《九章算术》卷九“勾股”中记载:今有户不知高广,竿不知长短,横之不出四尺,纵之不出二尺,斜之适出,问户斜几何. 如图,在△ABC中,按以下步骤作图:
如图,在△ABC中,按以下步骤作图: