若不等式组$\left\{\begin{array}{l}{\frac{5x-3}{3}+3＞x}\\{x≤a}\end{array}\right.$的整数解有四个.则a的取值范围是( )A．a≥1B．1＜a≤2C．1≤a＜2D．1＜a＜2 题目和参考答案——青夏教育精英家教网—

题目内容

18．若不等式组$\left\{\begin{array}{l}{\frac{5x-3}{3}+3＞x}\\{x≤a}\end{array}\right.$的整数解有四个，则a的取值范围是（　　）

A．

a≥1

B．

1＜a≤2

C．

1≤a＜2

D．

1＜a＜2

分析先解每一个不等式，再根据不等式组解集的范围内有四个整数解，得出新的不等式，求a的取值范围．

解答解：$\left\{\begin{array}{l}{\frac{5x-3}{3}+3＞x①}\\{x≤a②}\end{array}\right.$，
解不等式①得x＞-3，
解不等式②得x≤a，
∵不等式组有四个整数解，即为-2，-1，0，1，
∴1≤a＜2，
故选C．

点评本题考查了一元一次不等式组的整数解．关键是先解每一个不等式，再根据整数解的个数，确定含a的代数式的取值范围．

练习册系列答案

（1）本次参加抽样调查的居民有多少人？
（2）将不完整的条形图补充完整．
（3）若居民区有8000人，请估计爱吃D粽的人数？

9．式子$\sqrt{\frac{1}{x-1}}$有意义，则x的取值范围是x＞1．

6．我国南海海域面积为3 500 000km²，用科学记数法表示正确的是（　　）

3.5×10⁶km²

3.5×10⁷km²

3.5×10⁸km²

3.5×10⁹km²

13．

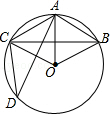如图，在半径为6cm的⊙O中，点A是劣弧$\widehat{BC}$的中点，点D是优弧$\widehat{BC}$上一点，且∠D=30°．
（1）求弦BC的长及sin∠AOB的值；
（2）求证：四边形ABOC是菱形．

3．

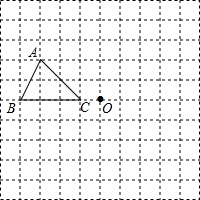在如图的方格中，每个小方格都是边长为1个单位的正方形，△ABC的三个顶点都在格点上（每个小方格的顶点叫格点）
（1）画出△ABC向下平移4个单位后的△A₁B₁C₁；
（2）画出△ABC绕点O顺时针旋转90°后的△A₂B₂C₂，并求线段OA在旋转过程中点A经过的路径长（结果用含有π和二次根式的式子表示）．

10．（1）如图1，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF=BE．求证：CE=CF；
（2）如图2，在正方形ABCD中，E是AB上一点，G是AD上一点，如果∠ECG=45°，求证：S_△ECG=S_△BCE+S_△CDG．

7．若$\frac{a+b}{c}$=$\frac{b+c}{a}$=$\frac{a+c}{b}$=k，则一次函数y=kx+x必经过（　　）

8．边长为2的正三角形的面积是$\sqrt{3}$．

试题分类