题目内容
16.对于反比例函数y=-$\frac{9}{x}$,下列说法正确的是( )| A. | 图象经过点(-3,-3) | |
| B. | 图象与x轴相交,但不与y轴相交 | |
| C. | 图象的两个分支分布在第二、四象限 | |
| D. | y随x的增大而增大 |
分析 根据反比例函数图象上点的坐标特征对A进行判断;根据反比例函数的性质对B、C、D进行判断.
解答 解:A、反比例函数y=-$\frac{9}{x}$的图象经过点(-3,3),所以A选项的说法不正确;
B、反比例函数y=-$\frac{9}{x}$的图象不与x轴相交,不与y轴相交,所以B选项的说法不正确;
C、反比例函数y=-$\frac{9}{x}$的图象的两个分支分布在第二、四象限,所以C选项的说法正确.
D、反比例函数y=-$\frac{9}{x}$,在每一象限,y随x的增大而增大,所以D选项的说法不正确.
故选C
点评 本题考查了反比例函数的性质:反比例函数y=xk(k≠0)的图象是双曲线;当k>0,双曲线的两支分别位于第一、第三象限,在每一象限内y随x的增大而减小;当k<0,双曲线的两支分别位于第二、第四象限,在每一象限内y随x的增大而增大.

练习册系列答案
相关题目
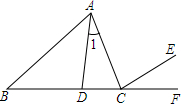
1. 如图,将直角三角形ABC的直角顶点C放在直线EF上,若∠BCF=36°,则∠ACE的度数是( )
如图,将直角三角形ABC的直角顶点C放在直线EF上,若∠BCF=36°,则∠ACE的度数是( )
 如图,将直角三角形ABC的直角顶点C放在直线EF上,若∠BCF=36°,则∠ACE的度数是( )
如图,将直角三角形ABC的直角顶点C放在直线EF上,若∠BCF=36°,则∠ACE的度数是( )| A. | 44° | B. | 46° | C. | 54° | D. | 56° |
5.要使$\frac{1}{4}$x2+25y2成为一个完全平方式,则应加上的一项为( )
| A. | ±10xy | B. | ±5xy | C. | 20xy | D. | $\frac{5}{2}$xy |
 根据给出图回答下列问题:
根据给出图回答下列问题: