题目内容
11.计算:$\frac{{(x}^{2}-{y}^{2})^{3}}{{x}^{2}+{y}^{2}}$÷$\frac{({x}^{2}+2xy+{y}^{2})^{2}}{{x}^{4}-{y}^{4}}$•($\frac{x+y}{{x}^{2}-2xy+{y}^{2}}$)分析 把除法化为乘法,分子、分母进行因式分解,根据约分法则计算即可.
解答 解:原式=$\frac{(x+y)^{3}(x-y)^{3}}{{x}^{2}+{y}^{2}}$•$\frac{({x}^{2}+{y}^{2})(x+y)(x-y)}{(x+y)^{4}}$•$\frac{x+y}{(x-y)^{2}}$
=(x+y)(x-y)2.
点评 本题考查的是分式的乘除运算,掌握运算法则、约分法则和因式分解是解题的关键.

练习册系列答案
相关题目
16.对于反比例函数y=-$\frac{9}{x}$,下列说法正确的是( )
| A. | 图象经过点(-3,-3) | |
| B. | 图象与x轴相交,但不与y轴相交 | |
| C. | 图象的两个分支分布在第二、四象限 | |
| D. | y随x的增大而增大 |
 在平面坐标系中,A(-1,5),B(-1,0),C(-4,3)
在平面坐标系中,A(-1,5),B(-1,0),C(-4,3)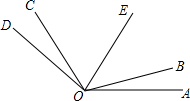 如图,已知OE是∠COA的平分线,∠AOE=59°35′,∠AOB=∠COD=16°17′22″.
如图,已知OE是∠COA的平分线,∠AOE=59°35′,∠AOB=∠COD=16°17′22″. 如图,OC平分∠AOB,OD平分∠AOC,已知∠AOD=15°,则∠BOC=30°.
如图,OC平分∠AOB,OD平分∠AOC,已知∠AOD=15°,则∠BOC=30°.