题目内容
如图，直线AB∥CD，若△ACO的面积为3cm2，则△BDO的面积为考点：平行线之间的距离
专题：几何图形问题
分析：过C作CM⊥AB于M，过D作DN⊥AB于N，求出CM=DN，得出S△ACB=S△BDA，都减去△AOB的面积即可得出答案．
解答：解：
过C作CM⊥AB于M，过D作DN⊥AB于N，
∵CD∥AB，
∴CM=DN，
∴S△ACB=S△BDA，
∴都减去△AOB的面积得：S△ACO=S△BDO=3cm2，
故答案为：3cm2
过C作CM⊥AB于M，过D作DN⊥AB于N，
∵CD∥AB，
∴CM=DN，
∴S△ACB=S△BDA，
∴都减去△AOB的面积得：S△ACO=S△BDO=3cm2，
故答案为：3cm2
点评：本题考查了平行线之间的距离和三角形面积的应用，关键是求出△ABC和△BDA的面积相等．
练习册系列答案
相关题目
如图所示，王师傅将两块相同的长方形木板AB，CD平行放置间隔一定距离，再用长、宽相等的两块铁片a，b分别搭在AB，CD上，再用螺丝固定，做成了一个简易的冰箱底垫．已知∠l=90°，用量角器度量出哪一个角，就可以判断铁片a与b是否为平行关系呢？
如图所示，若∠1=∠C=60°，∠D=120°，那么平行线有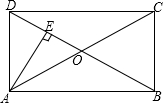
如图所示，已知矩形ABCD的对角线AC与BD相交于点0，AE丄BD于点E，且DE=OE，则∠OAB=
一木制门框高为2m，宽为1.5m，如图，要在门的对角线上加一根木条，则木条长为
如图所示，P是正方形对角线AC上一点，过点P分别作两组对边的垂线将正方形分为两个小正方形和两个矩形，如果正方形ABCD的周长为16，则图中两个小正方形的周长之和是
如图所示，要使l∥BC，补充条件