题目内容
 已知:如图,∠DAB=∠DCB,AF平分∠DAB,CE平分∠DCB,∠FCE=∠CEB.试说明:AF∥CE.
已知:如图,∠DAB=∠DCB,AF平分∠DAB,CE平分∠DCB,∠FCE=∠CEB.试说明:AF∥CE.解:因为∠DAB=∠DCB(
又因为AF平分∠DAB,
所以
| 1 |
| 2 |
又因为CE平分∠DCB,
所以∠FCE=
所以∠FAE=∠FCE.
因为∠FCE=∠CEB,
所以
所以AF∥CE(
考点:平行线的判定
专题:推理填空题
分析:利用角平线的性质和等量代换,根据已知条件,得出∠FAE=∠CEB,判断得出AF∥CE,证得结论解决问题.
解答:解:因为∠DAB=∠DCB(已知),
又因为AF平分∠DAB,
所以∠FAE=
∠DAB(角平分线的性质).
又因为CE平分∠DCB,
所以∠FCE=
∠DCB(角平分线的性质).
所以∠FAE=∠FCE.
因为∠FCE=∠CEB,
所以∠FAE=∠CEB,
所以AF∥CE(同位角相等,两直线平行).
故答案为:已知;∠FAE,角平分线的性质;
∠DCB,角平分线的性质;∠FAE,∠CEB;同位角相等,两直线平行.
又因为AF平分∠DAB,
所以∠FAE=
| 1 |
| 2 |
又因为CE平分∠DCB,
所以∠FCE=
| 1 |
| 2 |
所以∠FAE=∠FCE.
因为∠FCE=∠CEB,
所以∠FAE=∠CEB,
所以AF∥CE(同位角相等,两直线平行).
故答案为:已知;∠FAE,角平分线的性质;
| 1 |
| 2 |
点评:此题考查了平行线性质和判定和角平分线定义的应用,主要考查学生的推理能力.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
下列各图中,不为轴对称图形的是( )
A、 |
B、 |
C、 |
D、 |
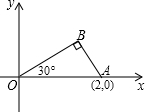 如图,已知O为坐标原点,∠AOB=30°,∠ABO=90°.且点A的坐标为(2,0).
如图,已知O为坐标原点,∠AOB=30°,∠ABO=90°.且点A的坐标为(2,0). 如图,已知△ABC.
如图,已知△ABC.