题目内容
 已知,Rt△ABC中,AC=BC=24,⊙O和边BC相切于点D.
已知,Rt△ABC中,AC=BC=24,⊙O和边BC相切于点D.(1)如图,∠C的平分线交边AB于点O,求证:AC与⊙O相切;
(2)当⊙O经过点A时,设点E,F分别为⊙O与边AC,AB的另一个交点,连接EF,若点E正好为AC的三等分点,求线段EF的长.
考点:切线的判定与性质
专题:
分析:(1)连接OC、OD,作OG⊥AC于E,根据等腰三角形三线合一,得出OA=OB,根据平行线的性质求得OD=
AC,OG=
BC,从而求得OG=OD,即可证得结论;
(2)作OM⊥AE,连接OD,先求得四边形MCDO是矩形,根据已知求得AE=16,EC=8,根据垂径定理求得AAM=ME=8,进而求得MC=OD=16,从而求得半径为16,进而求得直径EN=32,然后解等腰直角三角形的性质求得EF.
| 1 |
| 2 |
| 1 |
| 2 |
(2)作OM⊥AE,连接OD,先求得四边形MCDO是矩形,根据已知求得AE=16,EC=8,根据垂径定理求得AAM=ME=8,进而求得MC=OD=16,从而求得半径为16,进而求得直径EN=32,然后解等腰直角三角形的性质求得EF.
解答: (1)证明;如图1,连接OC、OD,作OG⊥AC于E,
(1)证明;如图1,连接OC、OD,作OG⊥AC于E,
∵Rt△ABC中,AC=BC=24,OC平分∠ACB,
∴OA=OB,
∵BC是⊙O的切线,
∴OD⊥BC,
∴OD∥AC,
∴OD=
AC,
∵OG⊥AC,
∴OG∥BC,
∴OG=
BC,
∴OG=OD,
∴OG是⊙O的半径,
∴AC与⊙O相切;
(2)解:如图2,作OM⊥AE,连接OD,
∵点E正好为AC的三等分点,
∴AE=
AC=
×24=16,
∴EC=8,
∴ME=MA=8,
∴MC=16,
∵BC是切线,
∴OD⊥BC,
∴四边形MCDO是矩形,
∴OD=MC=16,
∴⊙O的半径为16,
∴EN=32,
∵Rt△ABC中,AC=BC=24,
∴∠A=∠B=45°,
∵∠A=∠N=45°,
∵EN是直径,
∴∠EFN=90°,
∴△EFN是等腰直角三角形,
∴EF=
EN=
×32=16
.
 (1)证明;如图1,连接OC、OD,作OG⊥AC于E,
(1)证明;如图1,连接OC、OD,作OG⊥AC于E,∵Rt△ABC中,AC=BC=24,OC平分∠ACB,
∴OA=OB,
∵BC是⊙O的切线,
∴OD⊥BC,
∴OD∥AC,
∴OD=
| 1 |
| 2 |
∵OG⊥AC,
∴OG∥BC,
∴OG=
| 1 |
| 2 |
∴OG=OD,
∴OG是⊙O的半径,
∴AC与⊙O相切;
(2)解:如图2,作OM⊥AE,连接OD,
∵点E正好为AC的三等分点,

∴AE=
| 2 |
| 3 |
| 2 |
| 3 |
∴EC=8,
∴ME=MA=8,
∴MC=16,
∵BC是切线,
∴OD⊥BC,
∴四边形MCDO是矩形,
∴OD=MC=16,
∴⊙O的半径为16,
∴EN=32,
∵Rt△ABC中,AC=BC=24,
∴∠A=∠B=45°,
∵∠A=∠N=45°,
∵EN是直径,
∴∠EFN=90°,
∴△EFN是等腰直角三角形,
∴EF=
| ||
| 2 |
| ||
| 2 |
| 2 |
点评:本题考查了等腰三角形的性质,切线的判定和性质,平行线的性质,矩形的判定和性质,三角形的中位线定理等,作出辅助线构建矩形是本题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
甲、乙两列火车长分别是150米和200米,它们相向行驶在平行的轨道上,已知甲车上某位乘客测得乙车在他窗口外经过的时间是10秒,那么乙车上的乘客看见甲车在他窗口经过的时间是( )
| A、5秒 | B、7.5秒 |
| C、8.5秒 | D、10秒 |
 体育测试时,九年级一名男生,双手扔实心球,已知实心球所经过的路线是某个二次函数图象的一部分,如果球出手处A点距离地面的高度为2m,当球运行的水平距离为6m时,达到最大高度5m的B处(如图),问该男生把实心球扔出多远?(结果保留根号)
体育测试时,九年级一名男生,双手扔实心球,已知实心球所经过的路线是某个二次函数图象的一部分,如果球出手处A点距离地面的高度为2m,当球运行的水平距离为6m时,达到最大高度5m的B处(如图),问该男生把实心球扔出多远?(结果保留根号) 如图,已知一次函数y=x-2与反比例函数y=
如图,已知一次函数y=x-2与反比例函数y= 如图,AB是⊙O的直径,∠ABC=45°,AC=AB,BC交⊙O于点D.
如图,AB是⊙O的直径,∠ABC=45°,AC=AB,BC交⊙O于点D.
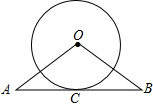 如图,AB与⊙O相切于点C,∠A=∠B,⊙O的半径为6,AB=16,求OA的长.
如图,AB与⊙O相切于点C,∠A=∠B,⊙O的半径为6,AB=16,求OA的长.