Question

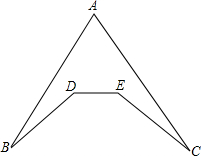某天，王梦洁从B村出发到C村找董倩，由于B村到C村之间有一小山，不能直接到达，现有两条路线可以选择，如图，一条路线是BDEC，另一条路线是BAC，请你就上述两条路线选择用一条从B村到C村的较近路线．

Answer 1

考点：三角形三边关系

专题：应用题

分析：延长BD交AC于点F，延长DE交AC于点G，先根据三角形三边关系比较BAC与BDFC路线，再比较BDFC与BDEGC路线，最后比较BDEGC路线与BDEC路线即可．

解答：解：BDEC路线较近．
理由：延长BD交AC于点F，延长DE交AC于点G，
在△ABF中，
∵AB+AF＞BF，
∴AB+AC＞BF+CF．
在△DFG中，
∵DF+FG＞DG，
∴BF+CF＞BD+DG+CG，
∴AB+AC＞BD+DG+CG．
在△CEG中，
∵EG+CG＞CE，DG＞DE，
∴BD+DG+CG＞BD+DE+CE，
∴AB+AC＞BD+DE+CE，
∴BDEC路线近．

点评：本题考查的是三角形的三边关系，熟知三角形任意两边之和大于第三边是解答此题的关键．