题目内容
如图，△ABC中，DE∥BC，DE=2，AD=4，DB=6，则BC的长是考点：相似三角形的判定与性质
专题：
分析：由平行可得对应线段成比例，即AD：AB=DE：BC，再把线段代入可求得BC．
解答：解：∵DE∥BC，
∴
=
，
∵AD=4，BD=6，
∴AB=10，
∴
=
，
解得BC=5，
故答案为：5．
∴
| AD |
| AB |
| DE |
| BC |
∵AD=4，BD=6，
∴AB=10，
∴
| 4 |
| 10 |
| 2 |
| BC |
解得BC=5，
故答案为：5．
点评：本题主要考查平行线分线段成比例的性质，掌握平行线分线段成比例中的对应线段是解题的关键．
练习册系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
如图，点B是线段AC上的一点，分别以AB、BC、CA为直径作半圆，求证：半圆AB的长与半圆BC的长之和等于半圆AC的长．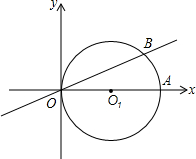
如图，在平面直角坐标系中圆O1的圆心在x轴上，直径OA=2，直线OB交圆O1于B，且∠BOA=15° 