题目内容
已知:如图,矩形ABCD中,AB >AD.

(1)以点A为圆心,AB为半径作弧,交DC于点E,且AE=AB,联结AE,BE,请补全图形,并判断∠AEB与∠CEB的数量关系;
(2)在(1)的条件下,设 ,
, ,试用等式表示a与b间的数量关系并加以证明.
,试用等式表示a与b间的数量关系并加以证明.
(1)∠AEB=∠CEB,作图见试题解析;(2) ,证明见试题解析.
,证明见试题解析.
【解析】
试题分析:(1)直接作出图形,由AE=BE=AB,得到△ABE是等边三角形,可以得到∠EAB=∠EBA=∠AEB=60°,进一步得到∠DEA=∠CEB=60°,故∠AEB=∠CEB;
(2)作过点A作AF⊥BE于点F,由 AB=AE,得到BF= BE,再证△ABF∽△BEC,有
BE,再证△ABF∽△BEC,有 ,即
,即 .
.
试题解析:(1)如图1,∠AEB=∠CEB.
(2) .证明如下:
.证明如下:
如图2,作过点A作AF⊥BE于点F,∵ AB=AE,∴BF= BE,∵∠AFB=∠C=90°,∠ABE=∠CEB,∴△ABF∽△BEC,∴
BE,∵∠AFB=∠C=90°,∠ABE=∠CEB,∴△ABF∽△BEC,∴ ,∴
,∴ ,即
,即 .
.


考点:1.矩形的性质;2.相似三角形的判定与性质.

练习册系列答案
相关题目
 ,求AB的长.
,求AB的长.

 B.1∶2 C.1∶4 D.1∶8
B.1∶2 C.1∶4 D.1∶8 与直线
与直线 的两个交点坐标分别为
的两个交点坐标分别为 ,
, ,则关于x的方程
,则关于x的方程 的解为__________.
的解为__________.

 B.
B. C.
C. D.
D.
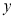 (件)与销售单价
(件)与销售单价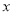 (元)之间满足
(元)之间满足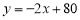 (20≤
(20≤ 的位置如图所示,则tanB的值为__________.
的位置如图所示,则tanB的值为__________.
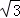 ≈1.732)
≈1.732)
