题目内容
3. 如图,长方体的底面边长分别为1cm和3cm,高为6cm,如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要多少cm?
如图,长方体的底面边长分别为1cm和3cm,高为6cm,如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要多少cm?
分析 要求所用细线的最短距离,需将长方体的侧面展开,进而根据“两点之间线段最短”得出结果.
解答  解:将长方体展开,连接A、B′,
解:将长方体展开,连接A、B′,
∵AA′=1+3+1+3=8(cm),A′B′=6cm,
根据两点之间线段最短,AB′=$\sqrt{{8}^{2}+{6}^{2}}$=10cm.
∴所用细线最短需要10cm.
点评 本题考查了平面展开-最短路径问题,本题就是把长方体的侧面展开“化立体为平面”,用勾股定理解决.

练习册系列答案
相关题目
13.下列各数中,互为相反数的是( )
| A. | -(-25)与-52 | B. | (-3)2与32 | C. | -3与-|-3| | D. | -6与(-2)×3 |
15.一个多边形的每个内角都是108°,那么这个多边形是( )
| A. | 五边形 | B. | 六边形 | C. | 七边形 | D. | 八边形 |
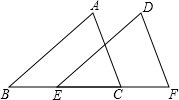 如图,点B、E、C、F在一条直线上,∠B=∠DEF,AB=DE,BE=CF,AC=6,则DF=6.
如图,点B、E、C、F在一条直线上,∠B=∠DEF,AB=DE,BE=CF,AC=6,则DF=6. 如图,AB=DC,BE=CF,AF=DE.求证:∠C=∠B.
如图,AB=DC,BE=CF,AF=DE.求证:∠C=∠B.