题目内容
18.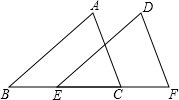 如图,点B、E、C、F在一条直线上,∠B=∠DEF,AB=DE,BE=CF,AC=6,则DF=6.
如图,点B、E、C、F在一条直线上,∠B=∠DEF,AB=DE,BE=CF,AC=6,则DF=6.
分析 先证明BC=EF,然后根据SAS证明△ABC≌△DEF,即可得到AC=DF=6.
解答 证明:∵BE=CF,
∴BC=EF,
在△ABC和△DEF中,
$\left\{\begin{array}{l}{BC=EF}\\{∠ABC=∠DEF}\\{AB=DE}\end{array}\right.$,
∴△ABC≌△DEF(SAS),
∴AC=DF,
∵AC=6,
∴DF=6.
故答案为:6.
点评 本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
6. 如图,已知MB=ND,∠MBA=∠NDC,下列条件不能判定△ABM≌△CDN的是( )
如图,已知MB=ND,∠MBA=∠NDC,下列条件不能判定△ABM≌△CDN的是( )
 如图,已知MB=ND,∠MBA=∠NDC,下列条件不能判定△ABM≌△CDN的是( )
如图,已知MB=ND,∠MBA=∠NDC,下列条件不能判定△ABM≌△CDN的是( )| A. | AM=CN | B. | AB=CD | C. | ∠M=∠N | D. | ∠A=∠NCD |
7.已知关于x的一元二次方程x2-x+m2-2m-5=0的一个根是-2,则m=( )
| A. | -1 | B. | 1 | C. | 2 | D. | -2 |
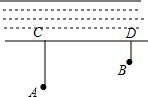 如图,牧童在A处放牛,其家在B处,A,B到河岸的距离分别为AC=400米,BD=200米,CD=800米,牧童从A处把牛牵到河边饮水后回家,问在何处饮水能使所走的总路程最短?最短路程是多少.
如图,牧童在A处放牛,其家在B处,A,B到河岸的距离分别为AC=400米,BD=200米,CD=800米,牧童从A处把牛牵到河边饮水后回家,问在何处饮水能使所走的总路程最短?最短路程是多少. 如图,长方体的底面边长分别为1cm和3cm,高为6cm,如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要多少cm?
如图,长方体的底面边长分别为1cm和3cm,高为6cm,如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要多少cm?