题目内容
8.将4个数a,b,c,d排成2行、2列,两边各加一条竖直线记成$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$,定义$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc,上述记号就叫做2阶行列式,若$|\begin{array}{l}{1-x}&{1+x}\\{1+x}&{1-x}\end{array}|$=12,则x=-3.分析 根据题中的新定义将所求的方程化为普通方程,整理后即可求出方程的解,即为x的值.
解答 解:根据题意化简$|\begin{array}{l}{1-x}&{1+x}\\{1+x}&{1-x}\end{array}|$=12,得
(x+1)2-(1-x)2=12,
整理得:x2+2x+1-(1-2x+x2)-12=0,
解得:x=-3.
故答案为:-3.
点评 此题考查了整式的混合运算,属于新定义的题型,涉及的知识有:完全平方公式,去括号、合并同类项法则,根据题意将所求的方程化为普通方程是解本题的关键.

练习册系列答案
相关题目
20.下列长度的三条线段能组成三角形的是( )
| A. | 1,2,4 | B. | 4,9,6 | C. | 5,5,11 | D. | 3,5,8 |
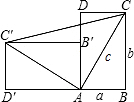 一个直立的火柴盒在桌面上倒下,启迪人们发现快乐勾股定理的一种新的证明方法,如图所示,火柴盒的一个侧面ABCD倒下到A′B′C′D′的位置,连接CC′.设AB=a,BC=b,AC=c,请利用此图证明勾股定理:a2+b2=c2.
一个直立的火柴盒在桌面上倒下,启迪人们发现快乐勾股定理的一种新的证明方法,如图所示,火柴盒的一个侧面ABCD倒下到A′B′C′D′的位置,连接CC′.设AB=a,BC=b,AC=c,请利用此图证明勾股定理:a2+b2=c2.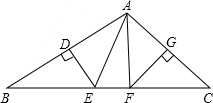 △ABC中,DE,FG分别垂直平分边AB,AC,垂足分别为点D,G.
△ABC中,DE,FG分别垂直平分边AB,AC,垂足分别为点D,G. 如图,长方体的底面边长分别为1cm和3cm,高为6cm,如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要多少cm?
如图,长方体的底面边长分别为1cm和3cm,高为6cm,如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要多少cm?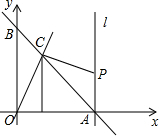 如图,直线y=-x+6与坐标轴交于A、B两点,与直线y=2x交于C点,直线是过A点且垂直x轴的直线,点P是直线l上的一动点.
如图,直线y=-x+6与坐标轴交于A、B两点,与直线y=2x交于C点,直线是过A点且垂直x轴的直线,点P是直线l上的一动点.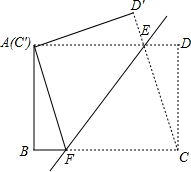 如图,将矩形ABCD沿直线EF折叠,使点C与点A重合,折痕交AD于点E、交BC于点F,连接AF、CE.①AF=CD′;②△CEF是等腰三角形;③四边形AFCE为菱形;④设AE=a,ED=b,DC=c,则a、b、c三者之间的数量关系为a2=b2+c2,其中正确的结论是②③④(将所有正确结论的序号都填在横线上)
如图,将矩形ABCD沿直线EF折叠,使点C与点A重合,折痕交AD于点E、交BC于点F,连接AF、CE.①AF=CD′;②△CEF是等腰三角形;③四边形AFCE为菱形;④设AE=a,ED=b,DC=c,则a、b、c三者之间的数量关系为a2=b2+c2,其中正确的结论是②③④(将所有正确结论的序号都填在横线上)