题目内容
6. 如图,△ABC中,D在BC上,AB=AD,AE=AC,∠1=∠2.求证:∠EDC=∠1.
如图,△ABC中,D在BC上,AB=AD,AE=AC,∠1=∠2.求证:∠EDC=∠1.
分析 根据在△ABC中,D为BC上的一点,AB=AD,AE=AC,∠1=∠2,求证△AED≌△ACD,然后利用等量代换即可求的结论.
解答 证明:∵∠1=∠2,
∴∠1+∠DAC=∠2+∠DAC,
即∠BAC=∠DAE,
在△AED与△ACD中
$\left\{\begin{array}{l}{AB=AD}\\{∠BAC=∠DAE}\\{AE=AC}\end{array}\right.$,
∴△AED≌△ACD(SAS),
∴∠B=∠ADE,
∵AB=AD,
∴∠B=∠ADB,
∴∠B+∠ADB+∠EDC=∠B+∠ADB+∠1=180°,
∴∠1=∠EDC
点评 此题考查全等三角形的判定和性质,关键是对全等三角形的判定与性质和等腰三角形的判定的理解和掌握.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
3. 如图,若AB∥CD,则下列结论正确的是( )
如图,若AB∥CD,则下列结论正确的是( )
 如图,若AB∥CD,则下列结论正确的是( )
如图,若AB∥CD,则下列结论正确的是( )| A. | ∠D+∠3=180° | B. | ∠B+∠DAB=180° | C. | ∠1=∠2 | D. | ∠3=∠4 |
7. 如图,将周长为8cm的△ABC沿BC方向平移1cm得到△DEF,则四边形ABFD周长为( )
如图,将周长为8cm的△ABC沿BC方向平移1cm得到△DEF,则四边形ABFD周长为( )
 如图,将周长为8cm的△ABC沿BC方向平移1cm得到△DEF,则四边形ABFD周长为( )
如图,将周长为8cm的△ABC沿BC方向平移1cm得到△DEF,则四边形ABFD周长为( )| A. | 8cm | B. | 10cm | C. | 12cm | D. | 16cm |
 如图,∠A是⊙O的圆周角,∠A=60°,则∠BOC的度数为120°.
如图,∠A是⊙O的圆周角,∠A=60°,则∠BOC的度数为120°. 如图,已知EF过平行四边形ABCD的顶点C,分别交AB、AD的延长线于E、F,且DF=2cm,DA=5cm.BE=4cm.求CD的长.
如图,已知EF过平行四边形ABCD的顶点C,分别交AB、AD的延长线于E、F,且DF=2cm,DA=5cm.BE=4cm.求CD的长. 已知:抛物线C1:y=x2-2x-3.
已知:抛物线C1:y=x2-2x-3.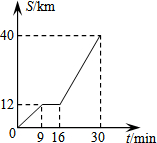 如图是某汽车行驶的路程S(km)与时间t(min)的函数关系图.观察图中所提供的信息,解答下列问题:
如图是某汽车行驶的路程S(km)与时间t(min)的函数关系图.观察图中所提供的信息,解答下列问题: