题目内容
先化简,再求值: 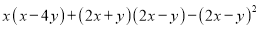 ,其中
,其中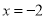 ,
, 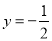 .
.
 【解析】试题分析:去括号,合并同类项,再把字母的值代入运算即可.
试题解析:原式,
,
当, 时,
原式.
【解析】试题分析:去括号,合并同类项,再把字母的值代入运算即可.
试题解析:原式,
,
当, 时,
原式.
练习册系列答案
 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
某班黑板是一个长方形,它的面积为6a2-9ab+3a,已知这个长方形的长为3a,则宽为_____.
 2a-3b+1
【解析】由题意可得,长方形的宽为:(6a2-9ab+3a)÷3a=2a-3b+1.
2a-3b+1
【解析】由题意可得,长方形的宽为:(6a2-9ab+3a)÷3a=2a-3b+1. 下列计算正确的是( )
A. 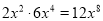 B.
B. 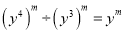 C.
C. 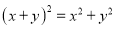 D.
D. 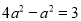
 B
【解析】选项A,原式=;选项B,原式= ;选项C, ;选项D,原式=3a2.故选B.
B
【解析】选项A,原式=;选项B,原式= ;选项C, ;选项D,原式=3a2.故选B. 用“●”“■”“”分别表示三种不同的物体,如图所示,前两架天平保持平衡,若要使第三架天平也平衡,那么“?”处应放“■”的个数为( )

A.2个 B.3个 C.4个 D.5个
 D
【解析】
试题分析:设“●”“■”“”分别为x、y、z,由图可知,
,解得x=2y,z=3y,
所以x+z=2y+3y=5y,即“■”的个数为5,
故选D.
D
【解析】
试题分析:设“●”“■”“”分别为x、y、z,由图可知,
,解得x=2y,z=3y,
所以x+z=2y+3y=5y,即“■”的个数为5,
故选D. 下列说法正确的是( )
A. 射线AB和射线BA表示同一条射线
B. 连接两点的线段叫做这两点之间的距离
C. 平角是一条直线
D. 射线可以看作直线的一部分
 D
【解析】试题分析:A、射线AB和射线BA端点不同,延伸方向不同,不是同一条射线,故此选项错误;
B、连接两点的线段的长度叫做这两点之间的距离,故此选项错误;
C、平角的特点是两条边成一条直线,不能说平角是一条直线,故本选项错误;
D、射线可以看作直线的一部分,故此选项正确.
故选D.
D
【解析】试题分析:A、射线AB和射线BA端点不同,延伸方向不同,不是同一条射线,故此选项错误;
B、连接两点的线段的长度叫做这两点之间的距离,故此选项错误;
C、平角的特点是两条边成一条直线,不能说平角是一条直线,故本选项错误;
D、射线可以看作直线的一部分,故此选项正确.
故选D. 观察下列运算并填空.
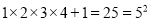 ;
;
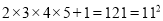 ;
;
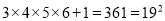 ;
; 
根据以上结果,猜想并研究: 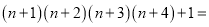 __________.
__________.
 【解析】试题解析:
…
故答案为: .
【解析】试题解析:
…
故答案为: . 计算: 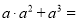 __________.
__________.
 【解析】试题解析:原式
故答案为: .
【解析】试题解析:原式
故答案为: . 向如图所示的正三角形区域扔沙包(区域中每一个小正三角形除颜色外完全相同),假设沙包击中每一个小三角形是等可能的,扔沙包1次击中阴影区域的概率等于_______.
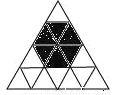
 【解析】由图可以看出,一共有最小规格的正三角形16个,其中涂黑了的有6个.有等可能的情况之下,扔沙包1次击中阴影区域的概率等于.故答案为: .
【解析】由图可以看出,一共有最小规格的正三角形16个,其中涂黑了的有6个.有等可能的情况之下,扔沙包1次击中阴影区域的概率等于.故答案为: . 已知,如图△ABC中,三条高AD、BE、CF相交于点O.若∠BAC=60°,求∠BOC的度数.
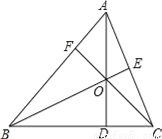
 120°.
【解析】试题分析:先根据三角形的内角和定理求出∠ABE、∠ACF的度数,再根据三角形内角和定理求出∠EBO+∠FCB的度数,即可求出∠BOC.
试题解析:在△ABC中,∵∠BAC=60°,三条高AD、BE、CF相交于点O.
∴∠BEA=90°,∠CFA=90°,
∴∠ABE=30°,∠ACF=30°,
∴∠OBD+∠OCB=180°﹣∠BAC﹣∠OBD﹣∠...
120°.
【解析】试题分析:先根据三角形的内角和定理求出∠ABE、∠ACF的度数,再根据三角形内角和定理求出∠EBO+∠FCB的度数,即可求出∠BOC.
试题解析:在△ABC中,∵∠BAC=60°,三条高AD、BE、CF相交于点O.
∴∠BEA=90°,∠CFA=90°,
∴∠ABE=30°,∠ACF=30°,
∴∠OBD+∠OCB=180°﹣∠BAC﹣∠OBD﹣∠... 
