题目内容
8.设二次函数y=-x2+x+b(b>0),当自变量为m时,其函数值大于0;当自变量为m-1、m+1时,其函数值分别为y1,y2,则( )| A. | y1>0,y2>0 | B. | y1>0,y2<0 | C. | y1<0,y2>0 | D. | y1<0,y2<0 |
分析 利用自变量x取m时对应的值大于0,确定m-1、m+1的位置,进而确定函数值为y1、y2.
解答 解:∵当自变量为m时,其函数值大于0,
∴m-1的最大值在左边交点之左,m+1的最小值在右边交点之右.
∴点(m+1,0)与(m-1,0)均在交点之外,
∴y1<0、y2<0.
故选D.
点评 本题考查了抛物线与x轴的交点和二次函数图象上的点的特征,解题的关键是确定点(m+1,0)与(m-1,0)均在交点之外.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
16.若反比例函数y=$\frac{k}{x}$(k≠0)经过(-2,3),则这个反比例函数一定经过( )
| A. | (-2,-3) | B. | (3,2) | C. | (3,-2) | D. | (-3,-2) |
13.一块砖的质量为m,体积为V,分成大小不等的两块,质量分别为m1,m2(m1>m2),体积分别为V1,V2,则( )
| A. | $\frac{m}{V}$=$\frac{{m}_{1}}{{V}_{1}}$=$\frac{{m}_{2}}{{V}_{2}}$ | B. | $\frac{m}{V}$>$\frac{{m}_{1}}{{V}_{1}}$>$\frac{{m}_{2}}{{V}_{2}}$ | ||
| C. | $\frac{{m}_{1}}{{V}_{1}}$=$\frac{{m}_{2}}{{V}_{2}}$≤$\frac{m}{V}$ | D. | $\frac{{m}_{2}}{{V}_{2}}$=$\frac{{m}_{1}}{{V}_{1}}$≥$\frac{m}{V}$ |
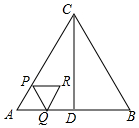 如图,△ABC是等边三角形,AB=4cm,CD⊥AB于点D,动点P从点A出发,沿AC以1cm/s的速度向终点C运动,当点P出发后,过点P作PQ∥BC交折线AD-DC于点Q,以PQ为边作等边三角形PQR,设四边形APRQ与△ACD重叠部分图形的面积为S(cm2),点P运动的时间为t(s).
如图,△ABC是等边三角形,AB=4cm,CD⊥AB于点D,动点P从点A出发,沿AC以1cm/s的速度向终点C运动,当点P出发后,过点P作PQ∥BC交折线AD-DC于点Q,以PQ为边作等边三角形PQR,设四边形APRQ与△ACD重叠部分图形的面积为S(cm2),点P运动的时间为t(s).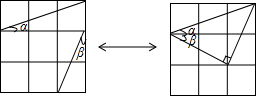
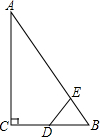 如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B的方向运动,设E点的运动时间为t秒,连接DE,当△BDE是直角三角形时,t的值为2或3.5.
如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B的方向运动,设E点的运动时间为t秒,连接DE,当△BDE是直角三角形时,t的值为2或3.5.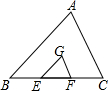 如图,点G是△ABC的重心,过G作GE∥AB,交BC于E,GF∥AC,交BC于F,则S△GEF:S△ABC=1:9.
如图,点G是△ABC的重心,过G作GE∥AB,交BC于E,GF∥AC,交BC于F,则S△GEF:S△ABC=1:9.