题目内容
抛物线y=x2-2x-3与x轴交于A、B两点(A在B的左边),与y轴交于点C,在其对称轴上有点P,当PA+PC取最小值时,P点坐标为 .
考点:抛物线与x轴的交点,轴对称-最短路线问题
专题:
分析:由两点之间线段最短可知当P点在线段AC上就可使PA+PC的值最小,再由P点要在对称轴上,可知P点应为线段AC与对称轴直线x=-1的交点,由(1)中求出的C点坐标即可得出抛物线的表达式,故可求出A、B两点的坐标,利用待定系数法即可求出直线AC的解析式,把x=-1代入即可求出P点坐标;
解答:解:如图,∵两点之间线段最短,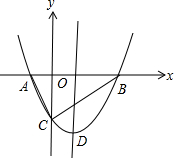
∴当P点在线段BC上就可使PA+PC的值最小.
又∵P点要在对称轴上,
∴P点应为线段BC与对称轴的交点,
∵y=x2-2x-3=(x-1)2-4,
∴对称轴x=1,
由抛物线的表达式为:y=x2-2x-3.
∴C(0,-3),
令y=0,则x2-2x-3=0.
解得:x1=3,x2=-1.
∴点A、B的坐标分别是A(-1,0)、B(3,0),
设直线BC的表达式为y=kx+b,则
解得
∴直线BC的表达式为y=x-3,
当x=1时,y=1×1-3=-2.
∴此时点P的坐标为(1,-2);
故答案为(1,-2).

∴当P点在线段BC上就可使PA+PC的值最小.
又∵P点要在对称轴上,
∴P点应为线段BC与对称轴的交点,
∵y=x2-2x-3=(x-1)2-4,
∴对称轴x=1,
由抛物线的表达式为:y=x2-2x-3.
∴C(0,-3),
令y=0,则x2-2x-3=0.
解得:x1=3,x2=-1.
∴点A、B的坐标分别是A(-1,0)、B(3,0),
设直线BC的表达式为y=kx+b,则
|
解得
|
∴直线BC的表达式为y=x-3,
当x=1时,y=1×1-3=-2.
∴此时点P的坐标为(1,-2);
故答案为(1,-2).
点评:本题考查了抛物线与x轴的交点,轴对称--最短路线问题,找到P点是本题的关键.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
某商品两次价格上调后,单位价格从4元变为4.84元,则平均每次调价的百分率是( )
| A、9% | B、10% |
| C、11% | D、12% |
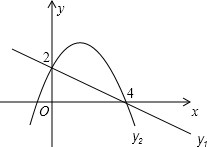 如图,已知直线y1=kx+n与抛物线y2=-x2+bx+c都经过A(4,0)和B(0,2).
如图,已知直线y1=kx+n与抛物线y2=-x2+bx+c都经过A(4,0)和B(0,2). 如图,点M、N是⊙O的弦AB的三等分点,过点M、N分别作AB的垂线,交弧AB的垂线于点C、D,那么
如图,点M、N是⊙O的弦AB的三等分点,过点M、N分别作AB的垂线,交弧AB的垂线于点C、D,那么