题目内容
1. 如图,四边形ABCD是平行四边形,E、F是对角线AC上的两点,连接BE、ED、DF、FB,若∠ADF=∠CBE=90°.
如图,四边形ABCD是平行四边形,E、F是对角线AC上的两点,连接BE、ED、DF、FB,若∠ADF=∠CBE=90°.(1)求证:四边形BEDF是平行四边形;
(2)若∠BAC=30°,∠BEC=45°,请判断AB与CE有什么数量关系,并说明理由.
分析 (1)只要证明△BCE≌△ADF,推出BE=DF,∠BEC=∠DFA,推出BE∥DF,由此即可证明;
(2)结论:AB=EC.作BH⊥AC于H.只要证明AB=2BH,EC=2BH即可解决问题;
解答  (1)证明:∵四边形ABCD是平行四边形,
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠BCE=∠DAF,
在△BCE和△DAF中,
$\left\{\begin{array}{l}{∠CBE=∠ADF=90°}\\{BC=AD}\\{∠BCE=∠DAF}\end{array}\right.$,
∴△BCE≌△ADF,
∴BE=DF,∠BEC=∠DFA,
∴BE∥DF,
∴四边形BEDF是平行四边形.
(2)结论:AB=EC.
理由:作BH⊥AC于H.
在Rt△ABH中,∵∠AHB=90°,∠BAH=30°,
∴AB=2BH,
在Rt△BEC中,∵∠EBC=90°,∠BEC=45°,BH⊥CE,
∴EH=HC,
∴EC=2BH,
∴AB=EC.
点评 本题考查平行四边形的判定和性质、全等三角形的判定和性质、直角三角形30度角性质、等腰直角三角形的性质等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.

练习册系列答案
相关题目
11.下列说法正确的是( )
| A. | x没有系数 | B. | π是单项式 | ||
| C. | x4+2x3是七次二项次 | D. | $\frac{3x-1}{5}$是单项式 |
10.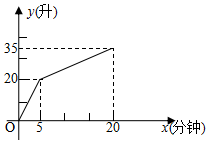 有一个附有进、出水管的容器,每单位时间进、出水量都是一定的,设从某时刻开始5分钟内只进水不出水,在随后的15分钟内既进水也出水,便得到x(分钟)与水量y(升)之间的关系如图.若20分钟后只放水不进水,则第( )分钟可将容器中的水放完?
有一个附有进、出水管的容器,每单位时间进、出水量都是一定的,设从某时刻开始5分钟内只进水不出水,在随后的15分钟内既进水也出水,便得到x(分钟)与水量y(升)之间的关系如图.若20分钟后只放水不进水,则第( )分钟可将容器中的水放完?
 有一个附有进、出水管的容器,每单位时间进、出水量都是一定的,设从某时刻开始5分钟内只进水不出水,在随后的15分钟内既进水也出水,便得到x(分钟)与水量y(升)之间的关系如图.若20分钟后只放水不进水,则第( )分钟可将容器中的水放完?
有一个附有进、出水管的容器,每单位时间进、出水量都是一定的,设从某时刻开始5分钟内只进水不出水,在随后的15分钟内既进水也出水,便得到x(分钟)与水量y(升)之间的关系如图.若20分钟后只放水不进水,则第( )分钟可将容器中的水放完?| A. | $\frac{95}{4}$ | B. | $\frac{95}{3}$ | C. | $\frac{95}{2}$ | D. | 95 |
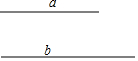 画图:已知线段a、b(不要求写画法,但要写出结论).
画图:已知线段a、b(不要求写画法,但要写出结论).