题目内容
1.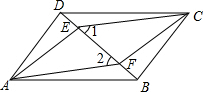 如图,四边形ABCD是平行四边形,E、F是对角线BD上的两点,∠1=∠2.
如图,四边形ABCD是平行四边形,E、F是对角线BD上的两点,∠1=∠2.(1)求证:DE=BF;
(2)求证:四边形AECF是平行四边形.
分析 (1)通过全等三角形△CDE≌△ABF的对应边相等证得DE=BF;
(2)根据平行四边形的判定定理:对边平行且相等的四边形是平行四边形证得结论.
解答  (1)证明:如图:∵四边形ABCD是平行四边形,
(1)证明:如图:∵四边形ABCD是平行四边形,
∴CD=AB,CD∥AB,
∴∠3=∠4,∵∠1=∠3+∠5,∠2=∠4+∠6,∠1=∠2
∴∠5=∠6
在△CDE与△ABF中,
$\left\{\begin{array}{l}{∠3=∠4}\\{CD=AB}\\{∠5=∠6}\end{array}\right.$,
∴△CDE≌△ABF(ASA),
∴DE=BF;
(2)证明:∵∠1=∠2,
∴CE∥AF.
又∵由(1)知,△CDE≌△ABF,
∴CE═AF,
∴四边形AECF是平行四边形.
点评 本题考查了全等三角形的判定与性质、平行四边形的判定与性质.平行四边形的判定方法共有五种,应用时要认真领会它们之间的联系与区别,同时要根据条件合理、灵活地选择方法.

练习册系列答案
相关题目
20.下列数值中不是不等式5x≥2x+9的解的是( )
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
9.下列平面图形中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
6.若(a-2)2+(b+3)2=0,则(a+b)2015的值是( )
| A. | 0 | B. | 1 | C. | -l | D. | 2012 |
13. 如图,∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A7B7A8的边长为( )
如图,∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A7B7A8的边长为( )
 如图,∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A7B7A8的边长为( )
如图,∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A7B7A8的边长为( )| A. | 6 | B. | 12 | C. | 32 | D. | 64 |
10. 如图,⊙O的直径CD⊥AB,∠CDB=25°,则∠AOC的度数为( )
如图,⊙O的直径CD⊥AB,∠CDB=25°,则∠AOC的度数为( )
 如图,⊙O的直径CD⊥AB,∠CDB=25°,则∠AOC的度数为( )
如图,⊙O的直径CD⊥AB,∠CDB=25°,则∠AOC的度数为( )| A. | 25° | B. | 30° | C. | 40° | D. | 50° |
11.在△ABC中,∠C=90°,sinA=$\frac{3}{5}$,D是AB的中点,则tan∠BCD+tan∠ACD=( )
| A. | $\frac{25}{12}$ | B. | 2 | C. | $\frac{4}{3}$ | D. | $\frac{8}{3}$ |
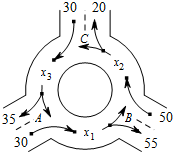 如图为某三岔路口交通环岛的简化模型.在某高峰时段,单位时间进出路口A,B,C的机动车辆数如图所示,图中x1,x2,x3分别表示该时段单位时间通过路段$\widehat{AB}$,$\widehat{BC}$,$\widehat{CA}$的机动车辆数(假设:单位时间内,在上述路段中,同一路段上驶入与驶出的车辆数相等),则x1,x2,x3的大小关系是x3>x1>x2.(用“>”、“<”或“=”连接)
如图为某三岔路口交通环岛的简化模型.在某高峰时段,单位时间进出路口A,B,C的机动车辆数如图所示,图中x1,x2,x3分别表示该时段单位时间通过路段$\widehat{AB}$,$\widehat{BC}$,$\widehat{CA}$的机动车辆数(假设:单位时间内,在上述路段中,同一路段上驶入与驶出的车辆数相等),则x1,x2,x3的大小关系是x3>x1>x2.(用“>”、“<”或“=”连接)