题目内容
12.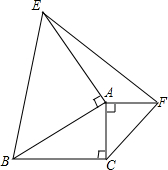 如图,Rt△ABC中,∠C=90°,△ABE,△AFC是等腰直角三角形,AB=5,AC=3,求EF长.
如图,Rt△ABC中,∠C=90°,△ABE,△AFC是等腰直角三角形,AB=5,AC=3,求EF长.
分析 在直角三角形ABC中,由AC与AB的长,利用勾股定理求出BC的长,延长FA,过E作延长线的垂线,垂足为D,利用同角的余角相等得到一对角相等,再由一对直角相等,且AE=AB,利用AAS得到三角形AED与三角形ABC全等,利用全等三角形对应边相等得到ED=BC,AD=AC,求出DF的长,在直角三角形EDF中,利用勾股定理求出EF的长即可.
解答 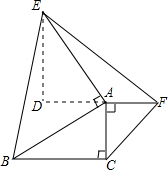 解:在Rt△ABC中,AB=5,AC=3,
解:在Rt△ABC中,AB=5,AC=3,
根据勾股定理得:BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=4,
延长FA,过E作延长线的垂线,垂足为D,
∴∠EAD+∠AED=90°,
∵∠FAC=∠ACB=90°,
∴∠DAC=90°,AD∥BC,
∴∠DAB=∠ABC,
∵∠EAD+∠BAD=90°,
∴∠EAD+∠ABC=90°,
∴∠AED=∠ABC,
在△AED和△ABC中,
$\left\{\begin{array}{l}{∠AED=∠ABC}\\{∠D=∠ACB=90°}\\{AE=AB}\end{array}\right.$,
∴△AED≌△ABC(AAS),
∴ED=BC=4,AD=AC=3,
在Rt△EDF中,ED=4,DF=AD+AF=3+3=6,
根据勾股定理得:EF=$\sqrt{E{D}^{2}+D{F}^{2}}$=$\sqrt{{4}^{2}+{6}^{2}}$=2$\sqrt{13}$.
点评 此题考查了全等三角形的判定与性质,以及勾股定理,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.已知点(-3,y1),(-2,y2),(2,y3)在函数y=$\frac{-1}{x}$的图象上,则( )
| A. | y1<y2<y3 | B. | y2<y1<y3 | C. | y3<y2<y1 | D. | y3<y1<y2 |
4.下列函数中,自变量x的取值范围是x>2的函数是( )
| A. | y=x-2 | B. | y=x2-4 | C. | y=$\frac{1}{x-2}$ | D. | y=$\frac{1}{{\sqrt{x-2}}}$ |
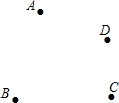 如图所示,已知平面上四个点A、B、C、D,按下列要求作图:别忘记了画图要用铅笔和直尺哦!!
如图所示,已知平面上四个点A、B、C、D,按下列要求作图:别忘记了画图要用铅笔和直尺哦!! 如图,已知AE=DB,BC=EF,AC=DF,求证:(1)AC∥DF;(2)CB∥EF.
如图,已知AE=DB,BC=EF,AC=DF,求证:(1)AC∥DF;(2)CB∥EF. 如图.已知点A(1,2)、B(4,1)、C(8,3).利用坐标网格和你的观察力.请直按说出△ABC外心的坐标和外接圆半径.
如图.已知点A(1,2)、B(4,1)、C(8,3).利用坐标网格和你的观察力.请直按说出△ABC外心的坐标和外接圆半径.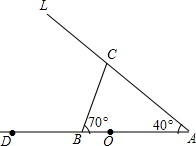 两只猎豹在如图的A处发现有一只野牛离群独自在O处觅食,猎豹打算用迂回的方式,由一只先从A前进到C处,然后再折回到B处截住野牛返回牛群的去路,另一只则直接从A处扑向野牛,已知∠BAC=40°,∠ABC=70°,问,猎豹从C处要转多少度才能直达B处?
两只猎豹在如图的A处发现有一只野牛离群独自在O处觅食,猎豹打算用迂回的方式,由一只先从A前进到C处,然后再折回到B处截住野牛返回牛群的去路,另一只则直接从A处扑向野牛,已知∠BAC=40°,∠ABC=70°,问,猎豹从C处要转多少度才能直达B处?