题目内容
9. 如图,在?ABCD中,DE平分∠ADC,AD=6,BE=2,则?ABCD的周长是( )
如图,在?ABCD中,DE平分∠ADC,AD=6,BE=2,则?ABCD的周长是( )| A. | 16 | B. | 14 | C. | 20 | D. | 24 |
分析 根据角平分线的定义以及两直线平行,内错角相等求出∠CDE=∠CED,再根据等角对等边的性质可得CE=CD,然后利用平行四边形对边相等求出CD、BC的长度,再求出?ABCD的周长.
解答 解:∵DE平分∠ADC,
∴∠ADE=∠CDE,
∵?ABCD中,AD∥BC,
∴∠ADE=∠CED,
∴∠CDE=∠CED,
∴CE=CD,
∵在?ABCD中,AD=6,BE=2,
∴AD=BC=6,
∴CE=BC-BE=6-2=4,
∴CD=AB=4,
∴?ABCD的周长=6+6+4+4=20.
故选:C.
点评 本题考查了平行四边形对边平行,对边相等的性质,角平分线的定义,等角对等边的性质,是基础题,准确识图并熟练掌握性质是解题的关键.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
20.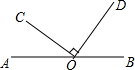 如图,点O在直线AB上,且OC⊥OD,若∠DOB=46°,则∠COA的大小是( )
如图,点O在直线AB上,且OC⊥OD,若∠DOB=46°,则∠COA的大小是( )
 如图,点O在直线AB上,且OC⊥OD,若∠DOB=46°,则∠COA的大小是( )
如图,点O在直线AB上,且OC⊥OD,若∠DOB=46°,则∠COA的大小是( )| A. | 34° | B. | 44° | C. | 54° | D. | 64° |
4.已知数据1,0,6,1,2,下列说法不正确的是( )
| A. | 中位数是6 | B. | 平均数是2 | ||
| C. | 众数是1 | D. | 最大值与最小值的差是6 |
18.下列运算正确的是( )
| A. | x2•x3=x6 | B. | 5x-2x=3x | C. | (x2)3=x5 | D. | (-2x)2=-4x2 |
2.已知点A(a,1)与B(-2,b)关于坐标原点对称,那么点P(a,b)绕原点顺时针旋转90°后的对应点P′的坐标是( )
| A. | (-1,2) | B. | (1,-2) | C. | (-1,-2) | D. | (1,2) |
 某经销商批发了一批无锡水蜜桃,为了打开销路,对1200个水蜜桃进行打包优惠出售,打包方式及售价如图,假设用这两种打包方式恰好装完全部水蜜桃.
某经销商批发了一批无锡水蜜桃,为了打开销路,对1200个水蜜桃进行打包优惠出售,打包方式及售价如图,假设用这两种打包方式恰好装完全部水蜜桃.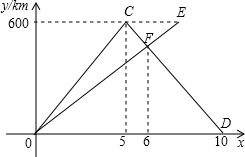 甲,乙两车同时从A城出发驶往B城,甲车到达B城后立即按原速返回A城,乙车继续行驶到B城,下面的图象反映的过程是离A城的距离y(km)与甲车行驶时间x(h)之间的函数关系.
甲,乙两车同时从A城出发驶往B城,甲车到达B城后立即按原速返回A城,乙车继续行驶到B城,下面的图象反映的过程是离A城的距离y(km)与甲车行驶时间x(h)之间的函数关系.