题目内容
 用6米的铝合金型材做个如图所示的矩形窗框,应做成长,宽各多少时,才能使做成的透光面积最大,最大透光面积是多少?
用6米的铝合金型材做个如图所示的矩形窗框,应做成长,宽各多少时,才能使做成的透光面积最大,最大透光面积是多少?考点:二次函数的最值
专题:
分析:设窗框的宽为xm,则宽为:(3-x)m,表示出面积利用二次函数最值求法得出即可.
解答:解:设窗框的宽为xm,则长为:
=(3-
x)m,设面积为S,根据题意可得:
S=x(3-
x)=-
x2+3x=-
(x-1)2+
.
当x=1时,y最大=
.
故最大的透光面积是:
.
答:当应做成长,宽分别是
、1时,才能使做成的透光面积最大,最大透光面积是
.
| 6-3x |
| 2 |
| 3 |
| 2 |
S=x(3-
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
当x=1时,y最大=
| 3 |
| 2 |
故最大的透光面积是:
| 3 |
| 2 |
答:当应做成长,宽分别是
| 3 |
| 2 |
| 3 |
| 2 |
点评:此题主要考查了二次函数最值求法,利用配方法求出是解题关键.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
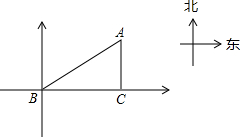 如图,一艘船由西向东航行,上午8时到达B处,看到有一灯塔在它的北偏东60°,距离为72海里的A处,上午10时到达C处,看到灯塔在它的正北方向,则这艘船航行的速度约为( )
如图,一艘船由西向东航行,上午8时到达B处,看到有一灯塔在它的北偏东60°,距离为72海里的A处,上午10时到达C处,看到灯塔在它的正北方向,则这艘船航行的速度约为( )| A、30海里/时 |
| B、31海里/时 |
| C、32海里/时 |
| D、33海里/时 |
 如图,已知∠1=∠2,∠A=∠F,试说明∠C=∠D.
如图,已知∠1=∠2,∠A=∠F,试说明∠C=∠D.