题目内容
已知圆锥底面圆的半径为3,高为3
,则它的全面积是 .
| 3 |
考点:圆锥的计算
专题:
分析:利用勾股定理易得圆锥的母线长,圆锥的侧面积=π×底面半径×母线长,然后加上底面圆的面积即可求得全面积.
解答:解:∵圆锥的底面半径是3,高是3
,
∴圆锥的母线长为6,
∴这个圆锥的侧面展开图的面积是π×3×6=18π,底面积为9π,
∴全面积为18π+9π=27π,
故答案为:27π.
| 3 |
∴圆锥的母线长为6,
∴这个圆锥的侧面展开图的面积是π×3×6=18π,底面积为9π,
∴全面积为18π+9π=27π,
故答案为:27π.
点评:考查圆锥的计算;掌握圆锥的侧面积的计算公式是解决本题的关键.

练习册系列答案
相关题目
若a+
b+2c=0,则关于x的方程ax2-bx+c=0(a≠0,且a≠2c)的根的情况是( )
| 2 |
| A、没有实数根 |
| B、有两个相等的实数根 |
| C、有两个不相等的实数根 |
| D、无法判断 |
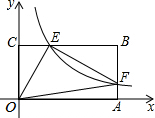 如图,A、C分别是x轴、y轴上的点,双曲线
如图,A、C分别是x轴、y轴上的点,双曲线