题目内容
17.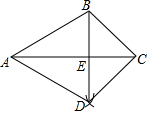 如图,已知△ABC.按如下步骤作图:①以A为圆心,AB长为半径画弧;②以C为圆心,CB长为半径画弧,两弧相交于点D;③连结BD,与AC交于点E,连结AD,CD.
如图,已知△ABC.按如下步骤作图:①以A为圆心,AB长为半径画弧;②以C为圆心,CB长为半径画弧,两弧相交于点D;③连结BD,与AC交于点E,连结AD,CD.(1)求证:△ABC≌△ADC;
(2)若∠BAC=30°,AB=4,求BE的长.
分析 (1)根据公共边与已知构成SSS可以证明两三角形全等;
(2)根据等腰三角形三线合一的性质证明△AEB是直角三角形,利用直角三角形30°角的性质得:BE=$\frac{1}{2}$AB=2.
解答 证明:在△ABC与△ADC中,
∵$\left\{\begin{array}{l}{AB=AD}\\{BC=CD}\\{AC=AC}\end{array}\right.$,
∴△ABC≌△ADC(SSS);
(2)解:∵△ABC≌△ADC,
∴∠BAE=∠DAE,
又∵AB=AD,
∴AE⊥BD,
∴∠AEB=∠AED=90°,
∵∠BAC=30°,
∴BE=$\frac{1}{2}$AB=2.
点评 本题考查了全等三角形的性质和判定、等腰三角形三线合一的性质、直角三角形30°角的性质,是常考题型,利用尺规作图的方式给出已知,所以注意阅读已知条件,熟练掌握等腰三角形三线合一的性质,在证明两三角形全等时,要注意找寻公共边、公共角、对顶角等条件;遇到30°角时,要考虑直角三角形30°角的性质的运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.下列代数式的书写格式正确的是( )
| A. | 1$\frac{1}{2}$abc | B. | n2 | C. | 3xy÷8 | D. | -$\frac{3}{4}$mn |
12.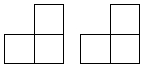 由一些大小相同的小正方形组成,下面的两个图分别是从正面和从上面看这个几何体得到的平面图形,那么组成该几何体所需的小正方形的个数为( )
由一些大小相同的小正方形组成,下面的两个图分别是从正面和从上面看这个几何体得到的平面图形,那么组成该几何体所需的小正方形的个数为( )
 由一些大小相同的小正方形组成,下面的两个图分别是从正面和从上面看这个几何体得到的平面图形,那么组成该几何体所需的小正方形的个数为( )
由一些大小相同的小正方形组成,下面的两个图分别是从正面和从上面看这个几何体得到的平面图形,那么组成该几何体所需的小正方形的个数为( )| A. | 4个 | B. | 4个或5个 | C. | 5个或6个 | D. | 6个 |
2.若a、b为相反数,c、d为倒数,|m|=4,则5cd-$\frac{a}{b}$-m的值是( )
| A. | 0或8 | B. | 0 | C. | 2 | D. | 10或2 |
9.矩形的对角线长10cm,顺次连结矩形四边中点所得四边形的周长为( )
| A. | 40 cm | B. | 10 cm | C. | 5 cm | D. | 20 cm |
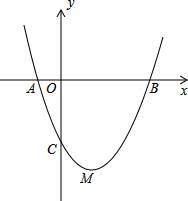 如图,在直角坐标系中,抛物线y=x2+bx-3与x轴交于A、B两点,与y轴于点C,顶点为M,已知A(-1,0).
如图,在直角坐标系中,抛物线y=x2+bx-3与x轴交于A、B两点,与y轴于点C,顶点为M,已知A(-1,0).