题目内容
8.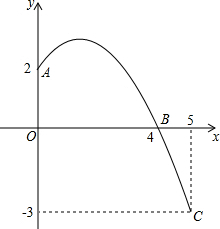 已知抛物线y=ax2+bx+c经过A,B,C三点,当x≥0时,图象如图所示,求出抛物线的表达式并写出其顶点坐标.
已知抛物线y=ax2+bx+c经过A,B,C三点,当x≥0时,图象如图所示,求出抛物线的表达式并写出其顶点坐标.
分析 根据图象确定A,B,C三点的坐标,进而代入抛物线解析式,然后求出a,b,c的值即可求得解析式,然后把解析式化简成顶点式可以得到顶点坐标.
解答 解:∵如图所示,抛物线经过A,B,C三点,
∴A(0,2),B(4,0),C(5,-3),
∴把A,B,C三点分别代入抛物线解析式中得:
$\left\{\begin{array}{l}{c=2}\\{16a+4b+c=0}\\{25a+5b+c=-3}\end{array}\right.$,
∴$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=\frac{3}{2}}\\{c=2}\end{array}\right.$,
∴抛物线的解析式为:y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2,即y=-$\frac{1}{2}$(x2-3x)+2,即y=-$\frac{1}{2}$(x-$\frac{3}{2}$)2+$\frac{25}{8}$,
∴抛物线的顶点坐标为:($\frac{3}{2}$,$\frac{25}{8}$).
点评 本题主要考查了待定系数法求二次函数的解析式以及二次函数的性质,解题的关键是熟练掌握待定系数法求函数的解析式,此题难度不大.

练习册系列答案
相关题目
1.已知y=x2+6x+m与y=(x-n)2是同一函数,则顶点是( )
| A. | (0,-3) | B. | (0,3) | C. | (-3,0) | D. | (3,0) |
 如图,在平面直角坐标系中,点O是坐标原点,AB⊥y轴于点D,AB=7,点B的横坐标为3,点C坐标为(5,0),连接CB,CB的延长线交y轴于点E,ED=6.
如图,在平面直角坐标系中,点O是坐标原点,AB⊥y轴于点D,AB=7,点B的横坐标为3,点C坐标为(5,0),连接CB,CB的延长线交y轴于点E,ED=6.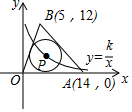 如图,点A(14,0),点B(5,12),P为△OAB内心,若反比例函数y=$\frac{k}{x}$的图象经过点P,则k=36.
如图,点A(14,0),点B(5,12),P为△OAB内心,若反比例函数y=$\frac{k}{x}$的图象经过点P,则k=36. 的平方根是_____.
的平方根是_____.