题目内容
 21、矩形ABCD中,AE平分∠BAC交BC于E,CF平分∠ACD交AD于F.
21、矩形ABCD中,AE平分∠BAC交BC于E,CF平分∠ACD交AD于F.(1)试说明四边形AECF为平行四边形;
(2)填空:当∠ACB=
30°
时,四边形AECF为菱形.分析:(1)先证明△ABE≌△CDF,再根据“由一组对边平行且相等的四边形是平行四边形”进行证明;
(2)根据EA=EC,推得∠ECA=∠BAE=∠EAC,从而得到∠ACB=30°.
(2)根据EA=EC,推得∠ECA=∠BAE=∠EAC,从而得到∠ACB=30°.
解答:(1)证明:∵∠BAC=∠DCA,AE平分∠BAC,CF平分∠ACD,
∴∠BAE=∠DCF,
∴AE∥CF,
∵AB=CD,∠B=∠D,
∴△ABE≌△CDF,
∴AE=CF,
∴四边形AECF为平行四边形;
(2)解:∵四边形AECF为菱形,
∴EA=EC,
∴∠EAC=∠ECA,∠BAE=∠EAC,
∴∠ECA=∠BAE=∠EAC=30°,即∠ACB=30°.
∴∠BAE=∠DCF,
∴AE∥CF,
∵AB=CD,∠B=∠D,
∴△ABE≌△CDF,
∴AE=CF,
∴四边形AECF为平行四边形;
(2)解:∵四边形AECF为菱形,
∴EA=EC,
∴∠EAC=∠ECA,∠BAE=∠EAC,
∴∠ECA=∠BAE=∠EAC=30°,即∠ACB=30°.
点评:考查到的知识点有:①三角形的全等;②平行四边形的判定;③菱形的性质.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
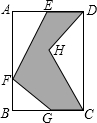 如图所示,在矩形ABCD中,AE=BG=BF=
如图所示,在矩形ABCD中,AE=BG=BF=| 1 |
| 2 |
| 1 |
| 3 |
| A、8 | B、12 | C、16 | D、20 |
 24、如图,在矩形ABCD中,AE⊥BD于E,∠DAE=3∠EAB,则∠EAC的度数为
24、如图,在矩形ABCD中,AE⊥BD于E,∠DAE=3∠EAB,则∠EAC的度数为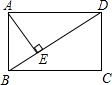 如图,矩形ABCD中,AE⊥BD于E,若BE=4,DE=9,则矩形的面积是
如图,矩形ABCD中,AE⊥BD于E,若BE=4,DE=9,则矩形的面积是 10、如图,在矩形ABCD中,AE⊥BD,垂足为E,∠DAE:∠BAE=1:2,则∠CAE=
10、如图,在矩形ABCD中,AE⊥BD,垂足为E,∠DAE:∠BAE=1:2,则∠CAE= 23、如图,在矩形ABCD中,AE⊥BD于E,∠DAE=2∠BAE,且AB=4cm.
23、如图,在矩形ABCD中,AE⊥BD于E,∠DAE=2∠BAE,且AB=4cm.