题目内容
计算:
(1)
÷(a-
)
(2)(x-y+
)(x+y-
)
(3)
-
=1.
(1)
| a-b |
| a |
| 2ab-b2 |
| a |
(2)(x-y+
| 4xy |
| x-y |
| 4xy |
| x+y |
(3)
| 2x |
| 2x-5 |
| 2 |
| 2x+5 |
考点:分式的混合运算,解分式方程
专题:
分析:(1)先算括号内的减法,再把除法化为乘法求解即可;
(2)先算括号内的加减,再算乘法求解即可;
(3)利用解分式方程步骤去分母,去括号,合并同类项,系数化为1,检验求解即可.
(2)先算括号内的加减,再算乘法求解即可;
(3)利用解分式方程步骤去分母,去括号,合并同类项,系数化为1,检验求解即可.
解答:解:(1)
÷(a-
)
=
•
=
;
(2)(x-y+
)(x+y-
)
=
•
=x2-y2;
(3)
-
=1.
方程两边同乘以(2x+5)(2x-5),得2x(2x+5)-2×(2x-5)=(2x+5)(2x-5),
去括号得4x2+10x-4x+10=4x2-25,
合并同类项得6x=-35,
系数化为1得x=-
经检验x=-
是原方程的根.
| a-b |
| a |
| 2ab-b2 |
| a |
=
| a-b |
| a |
| a |
| (a-b)2 |
=
| 1 |
| a-b |
(2)(x-y+
| 4xy |
| x-y |
| 4xy |
| x+y |
=
| (x+y)2 |
| x-y |
| (x-y)2 |
| x+y |
=x2-y2;
(3)
| 2x |
| 2x-5 |
| 2 |
| 2x+5 |
方程两边同乘以(2x+5)(2x-5),得2x(2x+5)-2×(2x-5)=(2x+5)(2x-5),
去括号得4x2+10x-4x+10=4x2-25,
合并同类项得6x=-35,
系数化为1得x=-
| 35 |
| 6 |
经检验x=-
| 35 |
| 6 |
点评:本题主要考查了分式的混合运算及解分式方程,解题的关键是熟记混合运算的顺序及解分式方程步骤.

练习册系列答案
相关题目
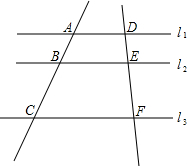 已知:如图,l1∥l2∥l3,则在下列比例中一定成立的是( )
已知:如图,l1∥l2∥l3,则在下列比例中一定成立的是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列说法中,错误的是( )
| A、邻补角的角平分线互相垂直 |
| B、平行于同一直线的两条直线互相平行 |
| C、在同一平面内不相交的两条直线一定平行 |
| D、经过一点有且只有一条直线与已知直线平行 |
将下列平面图形绕轴旋转一周,可得到圆锥的是( )
A、 |
B、 |
C、 |
D、 |
 如图,在△ABC中,AB=AC=8,BC=6,点D为BC上一点,BD=2.过点D作射线DE交AC于点E,使∠ADE=∠B.求线段EC的长度.
如图,在△ABC中,AB=AC=8,BC=6,点D为BC上一点,BD=2.过点D作射线DE交AC于点E,使∠ADE=∠B.求线段EC的长度.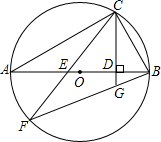 如图,已知AB是⊙O的直径,点C是⊙O上一点,连接BC,过点C作直线CD⊥AB于点D,弦CF与AB交于点E,弦BF与直线CD交于点G.已知BG=2,GF=4,求:BC的长度.
如图,已知AB是⊙O的直径,点C是⊙O上一点,连接BC,过点C作直线CD⊥AB于点D,弦CF与AB交于点E,弦BF与直线CD交于点G.已知BG=2,GF=4,求:BC的长度. 如图所示,AC是∠BAD的平分线,CE是∠ACD的平分线,那么图中相等的角有几对?分别是哪些角?
如图所示,AC是∠BAD的平分线,CE是∠ACD的平分线,那么图中相等的角有几对?分别是哪些角?