题目内容
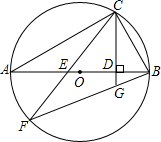 如图,已知AB是⊙O的直径,点C是⊙O上一点,连接BC,过点C作直线CD⊥AB于点D,弦CF与AB交于点E,弦BF与直线CD交于点G.已知BG=2,GF=4,求:BC的长度.
如图,已知AB是⊙O的直径,点C是⊙O上一点,连接BC,过点C作直线CD⊥AB于点D,弦CF与AB交于点E,弦BF与直线CD交于点G.已知BG=2,GF=4,求:BC的长度.考点:相似三角形的判定与性质,圆周角定理
专题:
分析:根据条件可得出∠BCG=∠F,可证得△BCG∽△BFC,再根据相似三角形的性质可得
=
,代入可求得BC.
| BG |
| BC |
| BC |
| BF |
解答:解:∵AB为⊙O的直径,CD⊥AB,
∴∠ACB=∠CDB=90°,
∴∠A+∠ACD=∠ACD+∠BCG=90°,
∵∠BCG=∠A,
又∵∠A=∠F,
∴∠BCG=∠F,且∠CBG=∠FBC,
∴△BCG∽△BFC,
∴
=
,
∵BG=2,GF=4,
∴BF=BG+GF=6,
∴
=
,
∴BC=2
.
∴∠ACB=∠CDB=90°,
∴∠A+∠ACD=∠ACD+∠BCG=90°,
∵∠BCG=∠A,
又∵∠A=∠F,
∴∠BCG=∠F,且∠CBG=∠FBC,
∴△BCG∽△BFC,
∴
| BG |
| BC |
| BC |
| BF |
∵BG=2,GF=4,
∴BF=BG+GF=6,
∴
| 2 |
| BC |
| BC |
| 6 |
∴BC=2
| 3 |
点评:本题主要考查相似三角形的判定和性质,根据条件证得△BCG∽△BFC是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
关于y的两个一元一次方程y+3m=32与y-4=1的解相同,那么m的值为( )
| A、9 | B、-9 | C、7 | D、-8 |
下列变形正确的是( )
| A、若3x-1=2x+1,则x=0 | ||||
| B、若ac=bc,则a=b | ||||
C、若a=b,则
| ||||
D、若
|
下列事件中是必然事件是( )
| A、实心铁球投入水中会沉入水底 |
| B、篮球队员在罚球线投篮一次,未投中 |
| C、明天太阳从西边升起 |
| D、抛出一枚硬币,落地后正面向上 |
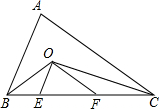 如图,△ABC中,BC=10cm,BO与CO分别为∠ABC与∠ACB的平分线,OE∥AB,OF∥AC,求△OEF的周长.
如图,△ABC中,BC=10cm,BO与CO分别为∠ABC与∠ACB的平分线,OE∥AB,OF∥AC,求△OEF的周长. 如图所示,一座楼房的楼梯,高1米,水平距离是2.8米,如果要在台阶上铺一种地毯,那么至少要买这种地毯
如图所示,一座楼房的楼梯,高1米,水平距离是2.8米,如果要在台阶上铺一种地毯,那么至少要买这种地毯