题目内容
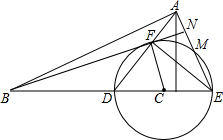 如图,在△ADE中,AE=DE,以DE中点C为圆心,CD为半径的圆分别交AD、AE于F、M两点.
如图,在△ADE中,AE=DE,以DE中点C为圆心,CD为半径的圆分别交AD、AE于F、M两点.(1)求证:AF=DF;
(2)过F作⊙C的切线交ED延长线于B,交AE于N,求证:BN⊥AE;
(3)连AB,若BD=9,且
| DF |
| DE |
| 3 |
| 5 |
考点:圆的综合题
专题:
分析:(1)由DE为圆C的直径可得EF⊥AD,再由等腰三角形的性质即可证明AF=DF;
(2)由圆的切线性质可得∠BFC=90°,进而可证明CF∥AE,所以∠BNE=∠BFC=90°,即BN⊥AE;
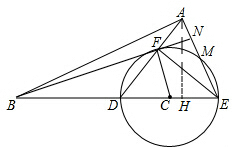
(3)作AH⊥BE,因为∠BFD=∠BEF,∠FBD=∠EBF,所以△BDF∽△BEF,由相似三角形的性质可得DF:EF=BD:BE,进而可求出BE=12,DE=BE-BD=12-9=3,所以DF=
,EF=
,利用S△ABD=
BD×AH计算即可.
(2)由圆的切线性质可得∠BFC=90°,进而可证明CF∥AE,所以∠BNE=∠BFC=90°,即BN⊥AE;
(3)作AH⊥BE,因为∠BFD=∠BEF,∠FBD=∠EBF,所以△BDF∽△BEF,由相似三角形的性质可得DF:EF=BD:BE,进而可求出BE=12,DE=BE-BD=12-9=3,所以DF=
| 9 |
| 5 |
| 12 |
| 5 |
| 1 |
| 2 |
解答:(1)证明:∵DE是直径,
∴∠DFE=90°,
即EF⊥AD,
∵AE=DE,
∴AF=DF
(2)证明:∵BN是圆C的切线,
∴CF⊥BF,
即∠BFC=90°,
∵EF⊥AD,
∴∠AEF=∠DEF=∠CEF,
∵CF=CE,
∴∠CFE=∠CEF=∠AEF,
∴CF∥AE,
∴∠BNE=∠BFC=90°,
∴BN⊥AE;
(3)∵△DEF是直角三角形,DF:DE=3:5,
∴DF:EF=3:4,
∵∠BFD=∠BEF,∠FBD=∠EBF,
∴△BDF∽△BFE,
∴DF:EF=BD:BF,即9:BE=3:4,
 ∴BE=12,
∴BE=12,
∴DE=BE-BD=12-9=3,
∴DF=
,EF=
∴AD=2DF=2×
=
作AH⊥BE,
∴EF×AD=DE×AH,
∴AH=EF×
=
,
∴S△ABD=
BD×AH=
×9×
=12.96.
∴∠DFE=90°,
即EF⊥AD,
∵AE=DE,
∴AF=DF
(2)证明:∵BN是圆C的切线,
∴CF⊥BF,
即∠BFC=90°,
∵EF⊥AD,
∴∠AEF=∠DEF=∠CEF,
∵CF=CE,
∴∠CFE=∠CEF=∠AEF,
∴CF∥AE,
∴∠BNE=∠BFC=90°,
∴BN⊥AE;
(3)∵△DEF是直角三角形,DF:DE=3:5,
∴DF:EF=3:4,
∵∠BFD=∠BEF,∠FBD=∠EBF,
∴△BDF∽△BFE,
∴DF:EF=BD:BF,即9:BE=3:4,
 ∴BE=12,
∴BE=12,∴DE=BE-BD=12-9=3,
∴DF=
| 9 |
| 5 |
| 12 |
| 5 |
∴AD=2DF=2×
| 9 |
| 5 |
| 18 |
| 5 |
作AH⊥BE,
∴EF×AD=DE×AH,
∴AH=EF×
| AD |
| DE |
| 216 |
| 75 |
∴S△ABD=
| 1 |
| 2 |
| 1 |
| 2 |
| 216 |
| 75 |
点评:本题考查了圆周角定理、切线的性质定理、勾股定理的运用、相似三角形的判定和性质、平行线的判定和性质以及垂直的判定和性质,题目的综合性较强,对学生的解题能力要求很高.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
关于x的方程2x+m=1的解是方程3x-2=2x-1的解的3倍,则m的值是( )
| A、-5 | B、-17 | C、1 | D、3 |
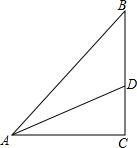 如图,△ABC中,AC=BC,AD平分∠BAC,若AC+CD=AB,求∠C的度数.
如图,△ABC中,AC=BC,AD平分∠BAC,若AC+CD=AB,求∠C的度数.