题目内容
已知关于x的一元二次方程x2+2px-p2-1=0的两个实数根为x1和x2.
(1)若此方程的两根之和不大于两根之积,求p的值;
(2)若p=-1,求x13+2x22+2x2的值.
(1)若此方程的两根之和不大于两根之积,求p的值;
(2)若p=-1,求x13+2x22+2x2的值.
考点:根与系数的关系,根的判别式
专题:计算题
分析:(1)根据根与系数的关系得到x1+x2=-2p,x1x2=-p2-1,则-2p≤-p2-1,变形有(p-1)2≤0,然后根据非负数的性质得p=1;
(2)当p=-1时,原方程变形为x2-2x-2=0,根据一元二次方程根的定义得到x12-2x1-2=0,x22-2x2-2=0,即x12=2x1+2,x22=2x2+2,原式可化简为x1(2x1+2)+2(2x2+2)+2x2=2x12+2x1+6x2+4=6(x1+x2)+8,然后根据根与系数的关系得到x1+x2=2,再利用整体代入的方法计算即可.
(2)当p=-1时,原方程变形为x2-2x-2=0,根据一元二次方程根的定义得到x12-2x1-2=0,x22-2x2-2=0,即x12=2x1+2,x22=2x2+2,原式可化简为x1(2x1+2)+2(2x2+2)+2x2=2x12+2x1+6x2+4=6(x1+x2)+8,然后根据根与系数的关系得到x1+x2=2,再利用整体代入的方法计算即可.
解答:解:(1)根据题意得x1+x2=-2p,x1x2=-p2-1,
∵方程的两根之和不大于两根之积,
∴-2p≤-p2-1,
即p2-2p+1≤0,
∴(p-1)2≤0,
∴p=1;
(2)当p=-1时,原方程变形为x2-2x-2=0,
∵x2-2x-2=0的两个实数根为x1和x2,
∴x12-2x1-2=0,x22-2x2-2=0,
即x12=2x1+2,x22=2x2+2,
∴x13+2x22+2x2=x1(2x1+2)+2(2x2+2)+2x2
=2x12+2x1+6x2+4
=2(2x1+2)+2x1+6x2+4
=6(x1+x2)+8,
∵x1+x2=2,
∴x13+2x22+2x2=6×2+8=20.
∵方程的两根之和不大于两根之积,
∴-2p≤-p2-1,
即p2-2p+1≤0,
∴(p-1)2≤0,
∴p=1;
(2)当p=-1时,原方程变形为x2-2x-2=0,
∵x2-2x-2=0的两个实数根为x1和x2,
∴x12-2x1-2=0,x22-2x2-2=0,
即x12=2x1+2,x22=2x2+2,
∴x13+2x22+2x2=x1(2x1+2)+2(2x2+2)+2x2
=2x12+2x1+6x2+4
=2(2x1+2)+2x1+6x2+4
=6(x1+x2)+8,
∵x1+x2=2,
∴x13+2x22+2x2=6×2+8=20.
点评:本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-
,x1x2=
.
| b |
| a |
| c |
| a |

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
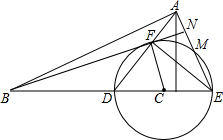 如图,在△ADE中,AE=DE,以DE中点C为圆心,CD为半径的圆分别交AD、AE于F、M两点.
如图,在△ADE中,AE=DE,以DE中点C为圆心,CD为半径的圆分别交AD、AE于F、M两点.