题目内容
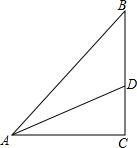 如图,△ABC中,AC=BC,AD平分∠BAC,若AC+CD=AB,求∠C的度数.
如图,△ABC中,AC=BC,AD平分∠BAC,若AC+CD=AB,求∠C的度数.考点:角平分线的性质,全等三角形的判定与性质
专题:
分析:在AB上截取AC=AE,设∠B=x°,求出∠BAC=∠B=x°∠EAD=∠CAD,根据SAS证△EAD≌△CAD,根据全等三角形的性质推出∠C=∠AED,CD=DE,求出BE=DE=DC,推出∠B=∠BDE=x°,求出∠C=2x°,在△ABC中由三角形的能较好的得x+x+2x=180°,求出即可.
解答: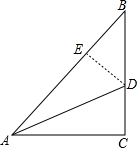 解:在AB上截取AC=AE,设∠B=x°,
解:在AB上截取AC=AE,设∠B=x°,
∵AC=BC,
∴∠BAC=∠B=x°
∵AD平分∠BAC,
∴∠EAD=∠CAD,
在△EAD和△CAD中
,
∴△EAD≌△CAD,
∴∠C=∠AED,CD=DE,
∵AC+CD=AB,AB-BE+AE,AE=AC,
∴BE=DE=DC,
∴∠B=∠BDE=x°,
∴∠C=∠AED=∠B+∠BDE=2x°,
在△ABC中,x+x+2x=180°,
∴x=45,
即∠C=2x°=90°.
 解:在AB上截取AC=AE,设∠B=x°,
解:在AB上截取AC=AE,设∠B=x°,∵AC=BC,
∴∠BAC=∠B=x°
∵AD平分∠BAC,
∴∠EAD=∠CAD,
在△EAD和△CAD中
|
∴△EAD≌△CAD,
∴∠C=∠AED,CD=DE,
∵AC+CD=AB,AB-BE+AE,AE=AC,
∴BE=DE=DC,
∴∠B=∠BDE=x°,
∴∠C=∠AED=∠B+∠BDE=2x°,
在△ABC中,x+x+2x=180°,
∴x=45,
即∠C=2x°=90°.
点评:本题考查了三角形内角和定理,全等三角形的性质和判定,等腰三角形的性质的应用,解此题的关键是①正确作辅助线,②求出∠C=2∠B.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
如果P点关于x轴的对称点是P′(-4,3),那么P点关于y轴的对称点是( )
| A、(-4,-3) |
| B、(4,-3) |
| C、(-4,3) |
| D、(4,3) |
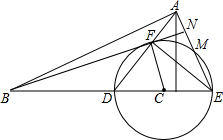 如图,在△ADE中,AE=DE,以DE中点C为圆心,CD为半径的圆分别交AD、AE于F、M两点.
如图,在△ADE中,AE=DE,以DE中点C为圆心,CD为半径的圆分别交AD、AE于F、M两点.