题目内容
求|x-1|+|x-2|+|x-3|+…+|x-2009|的最小值．
考点：绝对值
专题：
分析：当绝对值的个数为奇数时，取得最小值x是其中间项，而当绝对值的个数为偶数时，则x取中间两项结果一样．从而得出对于|x-1|+|x-2|+|x-3|+…+|x-2009|，当x=1005时取得最小值．
解答：解：由绝对值的几何意义可知，当绝对值的个数为奇数时，取得最小值x是其中间项，而当绝对值的个数为偶数时，则x取中间两项结果一样．
因此，对于|x-1|+|x-2|+|x-3|+…+|x-2009|，当x=1005时取得最小值，
此时原式=1004+1003+…+0+1+2+…+1004=1004×（1+1004）=1009020．
因此，对于|x-1|+|x-2|+|x-3|+…+|x-2009|，当x=1005时取得最小值，
此时原式=1004+1003+…+0+1+2+…+1004=1004×（1+1004）=1009020．
点评：此题主要考查了绝对值，培养学生运算求解能力，归纳能力，属于基础题．
练习册系列答案
中考解读考点精练系列答案
相关题目
如图是由几个棱长为1cm的小立方块搭成的几何体从上往下看的平面图形，小立方块中的数字表示该位置上小立方块的个数，求出这个几何体的体积．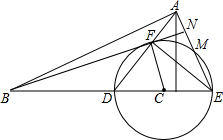
如图，在△ADE中，AE=DE，以DE中点C为圆心，CD为半径的圆分别交AD、AE于F、M两点．