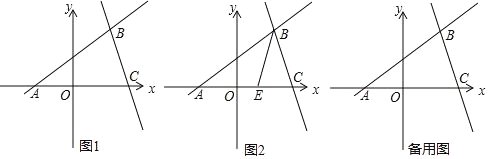
题目内容
【题目】如图1,AD为△ABC的中线,延长AD至E,使DE=AD.
(1)试证明:△ACD≌△EBD;
(2)用上述方法解答下列问题:如图2,AD为△ABC的中线,BMI交AD于C,交AC于M,若AM=GM,求证:BG=AC.

【答案】(1)详见解析;(2)详见解析.
【解析】
(1)根据中线的定义,即可得到BD=CD,再根据SAS即可判定△ACD≌△EBD.
(2)延长AD到F,使AD=DF,连接BF,根据SAS证△ADC≌△FDB,推出BF=AC,∠CAD=∠F,根据AM=GM,推出∠CAD=∠AGM=∠BGF,求出∠BGF=∠F,根据等腰三角形的性质求出即可.
(1)证明:∵AD是△ABC的中线,
∴BD=CD,
在△ACD和△EBD中,
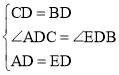 ,
,
∴△ACD≌△EBD(SAS).
(2)证明:延长AD到F,使AD=DF,连接BF,
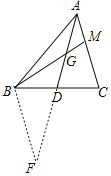
∵AD是△ABC中线,
∴BD=DC,
∵在△ADC和△FDB中
 ,
,
∴△ADC≌△FDB(SAS),
∴BF=AC,∠CAD=∠F,
∵AM=GM,
∴∠CAD=∠AGM,
∵∠AGM=∠BGF,
∴∠BGF=∠CAD=∠F,
∴BG=BF=AC,
即BG=AC.

练习册系列答案
相关题目